zadania na zbiorach nierówności Arek: A={x: x∊R i x²≤4} , B={x: x∊R i 2x²+6x−8>0} wyznacz A∩B , A∪B, A\B, B\A jak wyznaczyć zbiory A i B?

sylwia gdansk: A chyba bedzie (−∞.−2) suma(2;∞)

sylwia gdansk: a to B to masz kwadratowa to licz

Michał Szczotka: A będzie <−2;2>

sylwia gdansk: wlasnie kiedy jest tak jak ty podales a kiedy tak jak ja?bo sie zastanawiam

Michał Szczotka: B jest raczej okrągłe kwadratowe to jest może w cyrylicy

sylwia gdansk: sorki nei zauwazylam mniejsze lub rowne

Michał Szczotka: to wiesz czy nie wiesz

Arek: no ale jak liczyć B? będzie ok jak zrobię: 2x²+6x−8=0 ? 2x²+6x=8 x²+6x=4 x²+x=0,75 i co z tym dalej? jestem słaby z matematyki

Arek: B: x∊(0,5 ; ∞) dobrze?

Bogdan: Widzę, że to zadanko wisi już tu kilka godzin i efektu nie widać. No to rozwiążmy je. A = {x: x∊R i x² ≤ 4} x² − 4 ≤ 0 ⇒ (x − 2)(x + 2) ≤ 0 x=2 x=−2 + + + + −−−−− (−2) −−−−− (2) −−−−−>x − − A = <−2, 2> B={x: x∊R i 2x² + 6x − 8 > 0} 2x² + 6x − 8 > 0 ⇒ 2(x + 4)(x − 1) > 0 x=−4 x=1 + + + + −−−−− (−4) −−−−− (1) −−−−−>x − − B = (−∞, −4) U (1, +∞) Teraz trzeba wyznaczyć A∩B, A∪B, A\B, B\A.

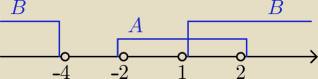
Bogdan: A = <−2, 2> B = (−∞, −4) U (1, +∞) A∩B = (1, 2> A∪B = (−∞, −4) ∪ <−2, +∞) A\B = <−2, 1> B\A = (−∞, −4) ∪ (2, +∞)

Arek: wielkie dzięki Bogdan.. uratowałeś mi życie