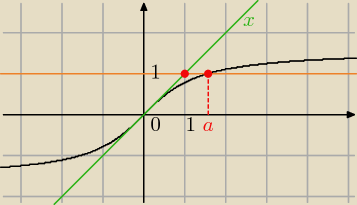
oblicz zdesperowana: bardzo prosze o pomoc oblicz pole obszaru ograniczonego krzywymi: y=arctgx, y=x, y=1. jak bedzie wyglądał gotowy wzór na pole z którego bede musiała wyliczyc rozwiazanie?

pigor: ... szukane pole P= 2 ∫ ₀^1₄π (arctgx−x)dx =

zdesperowana: jeśli mam dobrze rysunek to musze rozdzielić to na dwa pola tak?może mi napisać osobno wzór na to pierwsze i drugie pole? bo szczerze mówiąc ogólny wzór nic mi nie mówi...

zdesperowana: proszę, niech ktoś się mi pomoże

zdesperowana: pojutrze poprawka mógłby mi ktoś to wyliczyć po kolei, bo jestem sama nie dam rady..

Mila: Pomagam.

Mila:

	1
∫arctgxdx=xarctgx−		ln(1+x2)
	2

P₁=₀∫¹(x−arctg(x)dx=

	1		1
=[		x2−arctgx+		ln(1+x2)]01=dokończ, to sprawdzę.
	2		2

arctgx=1 / obustronnie tg ( tgx i arctgx funkcje odwrotne) tg(arctgx)=tg1 x=tg1=a P₂=₁∫^a(1−arctgx)dx= dokończysz?, spróbuj.

salma:

	1		π		1		1		1
P1 wyszło mi:		−		+		ln2 a P2 : −		ln I tg21+1I +		ln2
	2		4		2		2		2

	1		π		1
czyli P=		−		+		I tg21+1I ale nie jestem pewna czy dobrze. a powiedz mi skąd
	2		4		2

	1		1
się wzięło [		x2−arctgx+		ln(1+x2)]10 czy całka z (x−arctgx) była dobrze
	2		2

policzona?

zdesperowana:

	1		1
a nie źle ci napisałam P2 wyszło		ln(tg21+1)−		ln2 mam nadzieje że się nigdzie nie
	2		2

pomyliłam po drodze..

Mila: Całka z arctgx była dobrze policzona, ale źle podstawiłam, opuściłam x. (specjalnie napisałam CI całkę z arctgx, abyś miała możliwość sprawdzenia) Powinno być:

	1		1
P1=[		x2−xarctgx +		ln(x2+1)]01
	2		2

Policz jeszcze raz. policz P₂ Teraz muszę wyjść i będę po 22, to pomogę. Można to prościej zrobić, całkować po y. Nie wiem, czy tak uczyłaś się.

zdesperowana: obliczyłam jeszcze raz, powiedz, że się wszystko zgadza teraz

	1		π		1
P1:		−		+		ln2
	2		4		2

	1		π		1
P2: −tg1+		ln(tg21+1)+		−		ln2
	2		4		2

	1		1
P1+P2=		−tg1+		ln(tg21+1)
	2		2

Mila:

	1
∫(1−arctgx)dx= [x−xarctgx+		ln(1+x2} ]1tg1 granice (od 1 do tg1)
	2

P₂ policz

	1		1
P=		ln(1+tg21)−
	2		2

Mila: II sposób całkujemy po y. y=arctgx /obustronnie tg x=tgy Patrz na oś Y

	1		1
P=0∫1(tgy−y)dy=[−ln(cosy)−		y2]01=−ln(cos1)−		≈0,1156
	2		2

to jest taki sam wynik jak w poprzednim rozwiązaniu. Mam nadzieję, że nie zrobiłam literówek przy przepisywaniu.

zdesperowana: tzn że mój wynik jest poprawny? my na zajęciach nie używaliśmy tego II sposobu, więc poprzestanę na I ale dzięki serdeczne za pomoc.

zdesperowana: oj nie zauważyłam pierwszego wpisu, czyli wkradł mi sie mały błąd . czyli to P to już prawidłowy wynik ?

zdesperowana: wynik się zgadza, wielkie dzięki jeszcze raz za cierpliwość i pomoc

Mila: Zawsze pomogę, gdy ktoś tak ładnie dziękuje.