zamina całkowania - sprawdzenie Marek: Witam. Mam zadanie: zamienić kolejność całkowania w całce ∫²₀ dx ∫^x2−2x+2_{1−√2x−x²} f(x,y)dy rozrysowałem sobie i wychodzi mi: D: x = < 1−√1−(y−1)² , 1 + √y+1 > y= < 0, 2 > Bardzo proszę o sprawdzenie czy dobrze policzyłem

Artur_z_miasta_Neptuna: y = x² − 2x + 2 ⇔ y−1 = (x²−1)² ⇔ √y−1 = |x−1| i tutaj de facto musisz podzielić na dwa przedziały całkę (x∊<0;1> i x∊(1,2>)

Marek: A Czemu tak? Nie mogę zapisać tak jak w pierwszym poście?

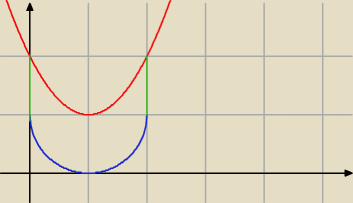
Krzysiek: rozbijasz na dwie całki ale dla: y∊[0,1] i y∊[1,2] a dlaczego? bo z lewej strony (jak i z prawej) obszar ograniczają dwie krzywe: "zielona" i "niebieska" wyznaczamy 'x' z równania: y=1−√2x−x² czyli: 2x−x² =(1−y)² (dla 1−y≥0 ) 1−(x−1)² =(1−y)² czyli: x=1+/− √1−(1−y)² zatem dla y∊[0,1] x∊[1−√1−(1−y)² ,1+√1−(1−y)² ] dla y∊[1,2] spróbuj Sam określić granice dla 'x'

Marek: Kurczę, nie rozumiem w jaki sposób wyszły Ci granice całkowania dla x W ogóle nie mogę sobie tego wyobrazić. Dolna granica to połowa okręgu, a górna?

Krzysiek: obie granice to ćwiartki okręgu po prostu z tego równania y=... musisz wyznaczyć x=... 1−(x−1)² =(1−y)² czyli: (x−1)² =1−(1−y)² pierwiastkujemy obustronnie: |x−1| =√1−(1−y)² czyli: x=1+√1−(1−y)² x=1−√1−(1−y)²

Marek: Ach tak, teraz rozumiem! Zapomniałem 'odwrócić' wykres A więc drugi obszar będzie ograniczony z dołu x=0 a z góry parabolą? D: x=< 0, 1 + √y−1 > y=< 1, 2 >

Krzysiek: nie z dołu i z góry tylko z lewej i prawej: więc z lewej x=0 a później ogranicza go krzywa: x=1−√y−1 następnie x=1+√y−1 i na końcu x=2 więc masz dwie całki dla y∊[1,2] lub dajesz jedną pomnożoną przez 2

Marek: Ok, rozumiem. Wielkie dzięki za wytłumaczenie