zad bak: oblicz długość przyprostokątnych trójkąta prostokątnego ABC, jesli tg α=4/3 i długośc przeciwprostokątnej równa się 15 cm.

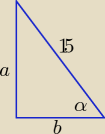
Artieeas: Chyba nie takie trudne Masz dany tangens α, ktory wynosi 4/3. Jest to nic innego jak stosunek przyprostokatnych trojkata. Mozesz wiec powiedziec, ze dlugosc jednej wynosi 4x a drugiej 3x, wtedy stosunek jest zachowany. Nastepnie korzystasz z twierdzenia pitagorasa a² + b² = c². Przyjmijmy, ze a=4x; b=3x, a c=15 Teraz liczysz... wychodzi 16x² + 9x² = 15² −> 25x² = 225 −> x² =9 −> x=3. Teraz podstawiasz... 4x= 4*3=12, 3x= 3*3=9. No i zdanie rozwiazane Jedna przyprostokatna ma dlugosc 12cm, a druga 9 cm.

Bogdan: Oczywiście dobrze, można też rozwiązać bez wprowadzania zmiennej x. Rozwiązujemy układ równań przy założeniach; a > 0 i b > 0.

	a		4		3
1.		=		⇒ b =		a
	b		3		4

	9		25
2. a2 + b2 = 225 ⇒ a2 +		a2 = 225 ⇒		a2 = 225 ⇒ a = 12
	16		16

	3
a = 12 oraz b =		*12 = 9
	4