zasady mnozenia-kombinatoryka
daga: rzucono monetami dwuzłotowa i pięciozłotową a następnie kostką. ile jest mozliwych wyników,
jesli na kostce wypadła liczba oczek nie mniejsza od 5.? zbiór wyników tego doswiadzcenia
przedsawt w postaci drzewka?
9 wrz 20:51
PW: Zacznijmy od liczenia. Nie ma tu żadnej wiedzy tajemnej, zwykłe mnożenie. Gdybyś miała na
kartce w kratkę obszar złożony z pięciu kolumn i sześciu wierszy, to wybór jednego z
kwadracików polega na:
!) wyborze kolumny (jednej z pięciu możliwych)
2) w wybranej kolumnie wskazaniu konkretnego kwadracika (jednego z sześciu).
Każdy, kto rozumie naturę mnożenia, wie, że kwadracików (możliwych zdarzeń) jest 5 razy 6.
Tu mamy podobnie: za pierwszym razem wybieramy jedną z dwóch możliwych stron monety 2−złotowej
(są dwie możliwości − orzeł lub reszka). Za drugim razem wybieramy jedną z dwóch możliwych
stron monety 5−złotowej (przypadkowo są znowu dwie możliwości − orzeł lub reszka)
Wszystkich możliwych zdarzeń jest więc 2 razy 2.
Kolejność rzucania nie ma znaczenia, tak jak nie miałoby znaczenia, czy wybieramy najpierw
kolumnę, czy wiersz na kartce, żeby wskazać konkretny kwadracik.
Dołączenie do tych czterech możliwych zdarzeń rzutu kostką powoduje, że zdarzeń będzie 4 razy
sześć (do każdego z czterech możliwych wyników rzutu dwiema kostkami dołączamy jeden z sześciu
wyników rzutu kostką. Tak więc mamy 2razy2razy6 wyników.
W tym zadaniu ograniczono wyniki rzutu kostka do dwóch (pięć oczek lub sześć), a więc wyników
jest 2razy2razy2..
Uczenie zapisuje się to, że wynikami doświadczenia są wszystkie możliwe trzyelementowe zbiory
{a1,a2,a3}, w których a1 mogą przybierać dwie wartości, a2 tak samo, zaś a3 mogą
przybierać sześć wartości.. Trzeba koniecznie zdawać sobie sprawę, że są to zbiory, a więc
kolejność zapisu nie ma tu żadnego znaczenia i nie wpływa na liczbę zdarzeń (to tak jakby przy
liczeniu objętości prostopadłościanu zmieniał kolejności mnożonych długości boków).
Drzewka nie narysuję, bo nie umiem rysować, ale zastanawiam się, po co. To nie w tego typu
zadaniach drzewka bywają użyteczne, choć ich dziwnie nie lubię, bo ogłupiają adeptów trudnej
sztuki prawdopodobieństwa.
Dosyć, bo zaczynam pisać podręcznik dla początkujących. A tak na marginesie: nie masz
podręcznika?
10 wrz 02:51
Aga1.:
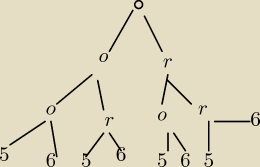
10 wrz 08:08
