Nierówność Aye: Siemka, po wakacjach zrobiły się luki w głowie i potrzebuje małej pomocy z waszej strony Mam problem z przykładem: (x−√2)²(x−2)²(x+√3)≥0

szklanka: (x−√2)²= x²−2√2x +2 (x−2)²= x²−4x+4 (x²−2√2x+2)(x²−4x+4)(x+√3)≥0 Obliczam deltę z dwóch pierwszych iloczynów pierwiastki wychodzą pierwszy iloczyn x₁=√2 drugi iloczyn x₂=2 trzeci iloczyn wyznaczam miejsce zerowe czyli x₃=√3 zaznacz na osi ten punktu , parabola do góry, a przedziałów szukaj na dole wykresu

Aga1.: odp.x∊<−√3,∞)

szklanka:

szklanka: oczywiście Agi rysunek jest poprawny!

Saizou : od parzystych pierwiastków wykres się odbija

Aga1.: Ta po lewej stronie gruba linia nie była przeze mnie rysowana. Szklanka trochę Cię wprowadza w błąd.

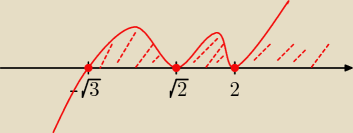
Gustlik: Szklanka − jedziesz do Rzymu przez Krym. Im bardziej rozłożony na czynniki wielomian, tym lepiej, a Ty go "składasz". (x−√2)²(x−2)²(x+√3)≥0 x=√2 − pierwiastek 2−krotny − wykres odbije się od osi, x=2 − pierwiastek 2−krotny − wykres odbije się od osi, x=−√3 − pierwiastek 1−krotny − wykres przetnie oś Pierwszy wyraz wielomianu: x²*x²*x=x⁵, st. 5 współczynnik kierunkowy dodatni, prawe ramię wykresu do góry Odp: x∊<−√3, +∞)

Eta: Ejj szklanko co Ty też wymyślasz (x−√2)²≥0 dla każdego x€R i (x−2)²≥0 dla x€R zatem x+√3 ≥0 ⇔ x ≥−√3 Rozwiązaniem tej nierówności jest: x€< −√3, ∞)

Eta: Wykres jest w tym przypadku zbyteczny

szklanka: pomyliłem się z wykresem tylko

Gustlik: Szklanka tam gdzie jest pierwiastek o parzystej krotności, czyli czynnik typu (x−a)^{do potęgi parzystej}, to wykres "odbija się" od osi OX, Przy pierwiastku o krotności nieparzystej czyli przy czynniku (x−a)^{do potęgi nieparzystej} wykres przecina oś OX. Wiecej na ten temat tutaj: https://matematykaszkolna.pl/strona/142.html . Wykres wielomianu zaczynamy rysować z prawej strony − od góry, gdy a>0 lub od dołu, gdy a<0. Prawe ramię wykresu wielomianu zachowuje się tak, jak ramiona paraboli, gdy a>0 (czyli współczynnik kierunkowy − ten przy pierwszym wyrazie) to prawe ramię leci w góre, a jak a<0 − prawe ramię leci w dół. Ot i cała filozofia rysowania wykresów wielomianów. A potem już łatwo.

Eta:

Aye: Dzięki wszystkim za pomoc z innymi przykładami już sobie poradzę