Geometria analityczna
Vizer: Mam zadanie:
Podaj równanie parametryczne i ogólne płaszczyzny prostopadłej do prostej:
{3x+4y+6z−5=0
{2x−6y−5z+5=0
która przecina tą prostą w punkcie o współrzędnej y=2.
Czy należy wyznaczyć wektor normalny do tej płaszczyzny i podstawić do równania prostej y=2 i
wyznaczyć z niego x i z, co nam już da równanie ogólne płaszczyzny, proszę o odpowiedź

Trivial:
Masz rację.
Najpierw wyznacz punkt przecięcia. Podstawiasz y=2:
| | ⎧ | 3x+6z = −3 | |
| | ⎨ | | → P = (1,2,−1)
|
| | ⎩ | 2x−5z = 7 | |
Teraz, postać krawędziową sprowadzasz do postaci parametrycznej.
| | ⎧ | 3x+4y+6z−5 = 0 | |
| L: | ⎨ | | → L: P0 + t*n = 0
|
| | ⎩ | 2x−6y−5z+5 = 0 | |
Nie interesuje nas P
0, tylko sam wektor
n. Podstawiamy x = t oraz pomijamy wyrazy wolne.
| | ⎧ | 4y+6z = −3t | |
| | ⎨ | |
|
| | ⎩ | −6y−5z = −2t | |
| | 27 | | 13 | | t | |
(x,y,z) = t*(1, |
| , − |
| ) = |
| (16, 27, −26) |
| | 16 | | 8 | | 16 | |
Zatem nasz wektor
n ma postać
n = (16, 27, −26). Dalej już prosto.


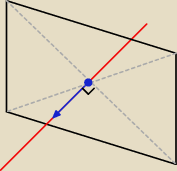 Może rysunek pomoże.
Może rysunek pomoże.  Czerwona linia to prosta podana w zadaniu.
Czerwona linia to prosta podana w zadaniu.

