Funkcja odwrotna Bartek: Znaleźć, o ile istnieje, funkcję odwrotną do f(x) = 3^x+2 − 5

ICSP: y = 3^x+2 − 5 y−5 = 3^x+2 log₃ (y−5) = x+ 2 x = log₃ (y−5) − 2 y = log₃ (x−5) − 2

Bartek: Dlaczego w drugiej linii jest y −5 ?

ICSP: omg Pozmieniaj na + i będzie dobrze Widocznie jeszcze się nie rozbudziłem Przepraszam

Bartek: powiedz mi skąd mam wiedzieć czy funkcja odwrotna istnieje czy nie ?

ICSP: funkcja odwrotna istnieje wtedy kiedy funkcja którą chcesz odwrócić jest różnowartościowa.

Bartek: Czy żeby sprawdzić czy funkcja jest różnowatościowa trzeba rysować wykres?

ICSP: Jeśli chcesz możesz Jednak na etapie liczenia funkcji odwrotnych powinieneś już wiedzieć które funkcje są różnowartościowe

Bartek: Dlaczego w ostatniej linii zamieniłeś X i Y ?

ICSP: aby można było ją narysować w układzie współrzędnych jako funkcję

Vax: ICSP sama różnowartościowość nie wystarcza, dana funkcja musi być jeszcze suriekcją (tj przeciwdziedzina ma być zbiorem wartości)

Bartek: Czy to zamienianie X z Y na końcu jest konieczne?

ICSP: Vax a przeciwdziedzina i zbiór wartości to nie jest to samo ?

Vax: Czyli na wyjściowym przykładzie funkcja f:R→R , f(x) = 3^x+2−5 nie jest odwracalna, za to f:R→(−5;+∞) , f(x) = 3^x+2−5 już jest odwracalna.

Vax: ICSP nie. Zbiór wartości jest podzbiorem przeciwdziedziny. Tj mając zapis f:R→R wiemy, że funkcja dla dowolnych rzeczywistych argumentów przyjmuje wartości rzeczywiste (to jest przeciwdziedzina), ale nie wiemy, czy dla każdego y z przeciwdziedziny znajdzie się takie x, że f(x) = y, np f:R→R f(x) = x² nie jest suriekcją, gdyż dla żadnego argumentu z dziedziny nie przyjmuje wartości np −1.

Bartek: Panowie spokojnie Powiedzcie mi tylko czy w ostatniej linijce muszę zamieniać X z Y czy można by było już tak zostawić

Vax: Bartek, ale chodzi o to, że f(x) = 3^x+2−5 w zależności od określenia dziedziny i przeciwdziedziny może być albo nie być odwracalne, przepisz całą treść

ICSP: czyli funkcja liniowa jest funkcją której przeciwdziedzina jest równa zbiorowi wartości ?

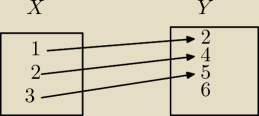
Aga1.: Przykład. Zbiór wartości funkcji {2,4,5} Przeciwdziedzina {2,4,5,6} {2,4,5}⊂{2,4,5,6}

Vax: Nie zawsze, np jak weźmiesz f:ℛ→ℂ takie, że f(x)=x to nie jest ona suriekcją, ponieważ dla żadnego argumentu z dziedziny nie przyjmuje wartości ,,i". Za to oczywiście dowolna niestała funkcja liniowa f:ℛ→ℛ jest suriekcją

ICSP: Dzięki za wyjaśnienie

Bartek: Mam problem jeszcze z dwoma przykładami, pomożecie? http://imageshack.us/photo/my-images/843/aaaafx.png/ zadanie 2 i 3 podpunkty c