Optymalizacja aa: Okno ma kształt obszaru wypukłego, będącego sumą prostokąta i półkola, którego średnicą jest górny bok prostokąta. Obwód okna jest równy k = 2,6 m. Wyznacz wymiary okna tak, aby przepuszczało ono jak najwięcej światła.

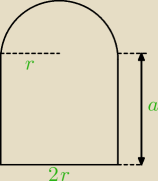
loitzl9006: Obwód takiego okna wynosi 2r+2a+πr = (2+π)r + 2a z treści zadania (2+π)r + 2a = 2,6 żeby okno przepuszczało jak najwięcej światła, to musi mieć jak największe pole

	πr2
Pole okna to P=2ar +		. Szukamy maksymalnej wartości tego wyrażenia.
	2

W tym celu wyznaczamy a z równania (2+π)r + 2a = 2,6

	(2+π)r
a=1,3 −
	2

wstawiamy do równania na pole i zauważamy że pole to funkcja kwadratowa zależna tylko od r, czyli P(r).

	(2+π)r		πr2
P(r)=2*(1,3 −		)r +
	2		2

upraszczasz wyrażenie i liczysz maksymalną wartość funkcji (współczynnik przy r² wychodzi ujemny zatem parabola ma ramiona skierowane w dół, funkcja przyjmuje wart. największą).

Aga1.: Wymiary prostokąta a=2r b=h, promień półkola r Obwód k=2r+2h+πr , r,h∊R₊ 2h+2r+πr=2,6

	1
h=1,3−r−		πr i h>0
	2

Pole powierzchni okna (pole prostokąta+pole półkola)

	1
P=2r*h+		πr2
	2

	1		1
P=2r(1.3−r−		πr)+		πr2
	2		2

	1
P=2,6r−πr2+		πr2
	2

	1
P(r)=−		πr2+2,6r
	2

	1
Pole jest opisane funkcją kwadratową a=−		π<0
	2

Funkcja osiąga wartość największą w wierzchołku

	b		−2,6		2,6
dla r=−		=		=
	2a		−π		π

Wymiary okna a=2r= b=h= dokończ i sprawdź rachunki ( nie wiem dlaczego nie ma napisów naniesionych na rysunek)