pliss pomocy kinia: rozwiąż nierównośc: (1 − logx) ² + (1 − logx) ³ + (1 − logx) ⁴ + ... ≤ 3 logx −1

kinia: ?

Gustlik: Ze wzoru na nieskończony szereg geometryczny:

	a1
S=		, gdy −1<q<1 ← warunek zbieżności szeregu.
	1−q

a₁=(1−logx)² q=1−logx

	(1−logx)2		(1−logx)2
S=		=
	1−1+logx		logx

Rozwiązujesz nierówność i założenia:

(1−logx)2
	≤3logx−1
logx

założenia: 1. −1<1−logx<1 (zbieżność szeregu) 2. x>o (dziedzina dla liczby logarytmowanej) 3. logx≠0 (mianownik) Wyznacz część wspólną tych założeń − będziesz miała dziedzinę tej nierówności. Dokończ... Jak nie będziesz wiedziała, pytaj.

kinia: mam problemy z nierównością....

kinia: dziedzina wyszła mi D= (1 , ∞) / {10}

kinia: jednak dziedzina to (100 , +∞) / {1}

kinia: chyba

Gustlik: Rozwiązujemy po kolei założenia: 1. −1<1−logx<1 (zbieżność szeregu) 2. x>o (dziedzina dla liczby logarytmowanej) 3. logx≠0 (mianownik) ad 1. −1<1−logx<1 /−1 −2<−logx<0 Rozbijam na układ 2 nierówności: −2<−logx /*(−1) −logx<0 /*(−1) 2>logx logx>0 logx<2 logx>0 logx<log10² logx>log10⁰ x<100 x>1 odp. zał. 1. x∊(1, 100) ad. 2. x>0 ⇒ x∊(0, +∞) − tu mamy "gotowca". ad. 3. logx≠0 logx≠log10⁰ x≠1 Część wspólna to x∊(1, 100) − mamy dziedzinę dla tej nierówności.

kinia: pomyliłam się w tym pierwszym założeniu, ale juz znalazłam błąd

kinia: tylko co teraz z tą nierównościa?

kinia: w tej nierówności tam gdzie jest kwadrat to mam skorzystac ze wzoru?

Gustlik: Teraz rozwiążę nierówność:

(1−logx)2
	≤3logx−1, D: x∊(1, 100)
logx

Podstawiam t=logx

(1−t)2
	≤3t−1, t≠0 (D)
t

(1−t)2
	−3t+1≤0
t

(1−t)2−3t2+t
	≤0
t

1−2t+t2−3t2+t
	≤0
t

−2t2−t+1
	≤0
t

Zamieniam na iloczyn licznika i mianownika (ten sam znak) i rozwiązuję jak nierówność wielomianową: t(−2t²−t+1)≤0 t=0 lub Δ=9, √Δ=3

	1−3		1
t1=		=−
	4		2

	1+3
t2=		=1
	4

t₃=0

	1
t∊<−		, 0)U<1, +∞)
	2

Przekształcam zapis "przedziałowy" na "nierównościowy

	1		1
t∊<−		, 0)U<1, +∞) ⇔ −		≤t<0 lub t≥1 ⇔
	2		2

	1
−		≤t
	2

i t<0 lub t≥1

	1
t≥−
	2

i t<0 lub t≥1 Wracam do podstawienia:

	1
1) logx≥−
	2

2) i logx<0 3) lub logx≥1

	1
ad 1) logx≥−
	2

	1
logx≥log10do potęgi −
	2

	1
x≥10do potęgi −
	2

	1		1
x≥(		)do potęgi
	10		2

	1
x≥√
	10

	√10
x≥		≈0,32
	10

ad 2) 2) i logx<0 logx<log10⁰ x<1 3) lub logx≥1 logx≥log10¹ x≥10

	√10
Mamy: (x≥		i x<1) lub x≥10
	10

	√10
czyli x∊<		, 1)∩<10, +∞) i do tego dziedzina x∊(1, 100)
	10

co daje odp: x∊<10, 100) (rys. u góry)

kinia: ma byc ze x∊<√10 , 100)

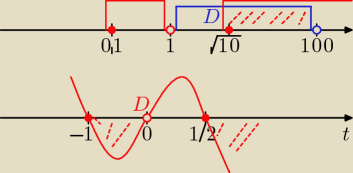Gustlik: Znalazłem chochlika, zgubiłem minus, sorry za pomyłke: t(−2t²−t+1)≤0 t=0 lub Δ=9, √Δ=3

	1−3		1
t1=		=
	−4		2

	1+3
t2=		=−1
	−4

t₃=0

	1
t∊<−1, 0)U<		, +∞)
	2

czyli 1) t≥−1 2) i t<0

	1
3) lub t≥
	2

1) logx≥−1 2) i logx<0

	1
3) lub logx≥
	2

ad 1) logx≥log10⁻¹ x≥0,1 i ad 2) logx<0 x<1 lub

	1
ad 3) logx≥
	2

	1
logx≥log10do potęgi
	2

x≥√10≈3,16 x∊<0,1; 1)U<√10, +∞) Odp: x∊<√10, 100) teraz jest dobrze. Jeszcze raz sorry, ale przy takiej ilosci obliczeń można coś zgubić.