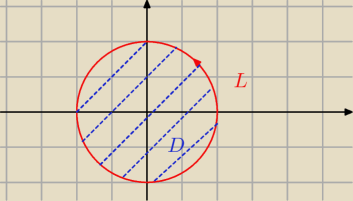
Green telo: Obliczyć całkę: ∫_L(2xy−y)dx+x²dy po krzywej: L = {(x, y) ∊ R² | x = 2cost, y=2sint, t ∊ <0; 2π>} Bardzo proszę aby ktoś pokazał jak to zrobić, korzystając z twierdzenia Greena

Trivial: Twierdzenie Greena

	∂Q		∂P
∫∂D Pdx + Qdy = ∬D (		−		)dxdy
	∂x		∂y

Przechodzimy na współrzędne biegunowe i od razu wyznaczamy granice

	⎧	0 ≤ r ≤ 2
G:	⎨
	⎩	0 ≤ φ ≤ 2π

I liczymy! ∫_L (2xy−y)dx + x²dy = ∬_D (2x − 2y−1)dxdy = ∬_G (2rcosφ − 2rsinφ−1)*rdrdφ = 2*∬_G r²(cosφ−sinφ) drdφ − ∬_G r drdφ = 0 − 2π*[¹₂r²]₀² = −4π całka z cosφ−sinφ w przedziale [0,2π] jest zerem

telo:

∂Q
	=2x
∂x

∂P
	=2x−1
∂y

2x − (2x − 1) = 2x − 2x + 1 = 1 Więc nie rozumiem dlaczego liczysz całkę: ∬D (2x − 2y−1)dxdy, czy mógłbyś mi to wytłumaczyć?

Trivial: Liczę taką całkę, bo się pomyliłem. W takim wypadku masz jeszcze prostszą sprawę i szybko policzysz, że taka całka to 4π.

telo: Dziękuję