logarytmy, pomocy

logarytmy, pomocy mania: rozwiąż równanie:

	2
1+ log₂sin2x + log²₂sin2x + log³₂sin2x + ... =		dla x∊<0,π>
	3

8 wrz 22:59

ZKS: a₁ = 1 q = log₂(sin(2x)) zał. sin(2x) > 0 ∧ |log₂(sin(2x))| < 1 Lewa strona suma nieskończonego ciągu geometrycznego.

	a₁
S_n =		.
	1 − q

8 wrz 23:03

mania: wychodzą mi jakieś głupoty...

8 wrz 23:12

mania: jak roziązac te założenia?

8 wrz 23:13

ZKS: Zapisz tutaj to zobaczy się jakie głupoty Ci wychodzą pokaż je to Ci się pomoże.

8 wrz 23:22

mania:

	1
to założenie z wartością bezwzględną w jednym wyszło że sin2x<2 i sin2x>
	2

8 wrz 23:37

mania: a to pierwsze założenie nie wiem jak zrobi..

8 wrz 23:38

ZKS:

	1
sin(2x) > −		zgubiłaś minus.
	2

Dla jakiego x spełniona jest nierówność sin(2x) < 2?

8 wrz 23:40

kinia: x=1

8 wrz 23:47

ZKS: Jeżeli x = 1 spełni nierówność sin(2x) < 2 to udowodnij to.

8 wrz 23:49

kinia: nie no nie spełni, nie pamiętam jak się juz to obliczało:(

8 wrz 23:52

ZKS: Właśnie o to chodzi że spełni nierówność x = 1. To powiedz jakie wartości może przyjmować sinus w jakim przedziale znajdują się wartości?

8 wrz 23:54

kinia: :(

8 wrz 23:58

ZKS: Wiesz czy nie wiesz?

8 wrz 23:59

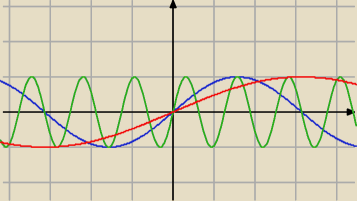
Piotr: rysunek

to dzięki b. emotka

9 wrz 00:00

ZKS: Piotr Ci nawet podpowiedział. emotka

9 wrz 00:02

mania:

π

2

9 wrz 00:05

ZKS: Odczytaj z rysunku który narysował Piotr zobacz że ta funkcja idzie od góry do dołu nie wychodząc poza pewne wartości.

9 wrz 00:08

mania:

	π
x∊(		+ 2kπ)
	2

9 wrz 00:09

mania: no nie wychodzi po za 1, my mamy odczytac dla ograniczonego bo dla x∊<0,π>

9 wrz 00:10

ZKS: Ty ciągle piszesz argument a ja chce żebyś odczytała jakie wartości przyjmuje sinus tylko i wyłącznie.

9 wrz 00:13

mania:

π

6

9 wrz 00:13

mania: <−1,1>

9 wrz 00:14

Piotr: emotka

9 wrz 00:15

ZKS: Właśnie czyli skoro nie wychodzi poza 1 i tutaj sam dopisze bo tego nie napisałaś −1 więc na pewno sin(2x) nie osiągnie wartości większej od 2 czyli x ∊ R.

	1
Teraz rozwiąż nierówność sin(2x) ≥ −		.
	2

9 wrz 00:15

ZKS:

	1
Przepraszam dobrze tam napisałaś że sin(2x) >		już widocznie zmęczony jestem.
	2

9 wrz 00:20

mania:

π		π
	,
6		2

9 wrz 00:31

ZKS: To jest przedział czy co?

9 wrz 00:36

ZKS:

	1
y =
	2

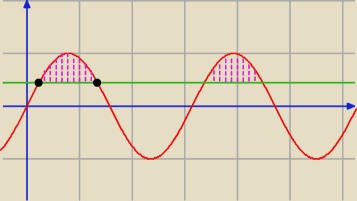y = sin(2x)

9 wrz 00:38

mania:

	π		π
(		+ kπ ,		+ kπ)
	6		2

9 wrz 00:38

ZKS:

π		5		1
	+ k * 2π < 2x <		+ k * 2π / *
6		6		2

π		5
	+ k * π < x <		+ k * π
12		12

jednak z góry mamy nałożone że x ∊ (0 ; π) więc ostatecznie

	π		5
x ∊ (		;		π)
	12		12

9 wrz 00:44

ZKS: Dokończ to Ci sprawdzę jak nie usnę.

9 wrz 00:45

mania: jeśli mogę wiedzziec to skończyłeś/aś już szkołe?

9 wrz 00:48

ZKS: A to nawet takie pytania masz do tego zadania? emotka

9 wrz 00:50

mania: ale ja nie wiem co dalej.

9 wrz 00:52

ZKS: Zapisz tutaj jak dokańczasz to zadanie to sprawdzę Ci.

9 wrz 00:53

mania: hehe nie nno to nie do zadania emotka

tak tylko pytam emotka

9 wrz 00:53

ZKS: Lewa strona to suma nieskończonego ciągu geometrycznego a wzór na to jest

	a₁
S_n =
	1 − q

gdzie: a₁ = 1 oraz q = log₂(sin(2x)).

9 wrz 00:55

ZKS: Oczywiście żartowałem z tamtym pytaniem. emotka

9 wrz 00:55

mania:

	1
no to to wiem, czyli mamy tak sn=
	1− log2(sin(2x))

	log₁0 10
sn=
	log₁0 10 − log2(sin(2x))

9 wrz 01:00

ZKS:

	1
Nic nie zamieniaj więc S_n =		czyli
	1 − log₂(sin(2x))

1		2
	=
1 − log₂(sin(2x))		3

9 wrz 01:04

mania: teraz mam przemnożyc na krzyż?

9 wrz 01:09

mania: nie mam pomysłu na to jak zrobic.

9 wrz 01:10

ZKS: A podaj jaki wynik jest w odpowiedzi.

9 wrz 01:10

mania:

	π		3
x =		v x =		π
	8		8

9 wrz 01:15

ZKS: Okej to za chwilę to napisze. emotka

9 wrz 01:16

ZKS:

1		2		3
	=		/ *		(1 − log₂(sin(2x)))
1 − log₂(sin(2x))		3		2

	3
1 − log₂(sin(2x)) =
	2

	1
log₂(sin(2x)) = −
	2

sin(2x) = 2^−¹/₂

	√2
sin(2x) =
	2

	π		3
2x =		+ k * 2π ∨ 2x =		π + k * 2π
	4		4

	π		3
x =		+ k * π ∨ x =		π + k * π
	8		8

Teraz sprawdzamy czy podane rozwiązania mieszczą się w naszej dziedzinie.

	π		π		5
x =		należy do przedziału (		;		π)
	8		12		12

	3		π		5
x =		π nie należy do przedziału (		;		π)
	8		12		12

Ostatecznie:

	π
x =		.
	8

9 wrz 01:19

mania: dzięki ci wiekie emotka

9 wrz 01:22

ZKS: Tylko zauważ że ja jedno rozwiązanie odrzuciłem a u Ciebie w odpowiedzi jest inaczej ponieważ dają dwie.

9 wrz 01:25

ZKS: Na zdrowie i dobranoc bo już idę na spanie. emotka

9 wrz 01:25

gielczunator: @ZKS: 1/12 < 3/8 < 5/12, obie poprawne

3 paź 18:32

5-latek: Witaj ZKS po 4 latach emotka

3 paź 18:43