Oblicz pole obszaru ograniczonego krzywymi y^2=x i y=x^3 Bart: Oblicz pole obszaru ograniczonego krzywymi y²=x i y=x³ {y² = x {y = x³ x = x³ x³ − x = 0 x(x² − 1) = 0 x = 0 v x² − 1 = 0 x² = 1 x = 1 v x = −1 |P|=

Bart: |P| = ∫₃√x dx − ∫₀ x³ dx = czy |P| = ∫¹ (√x − x³)dx =

Bart: ref

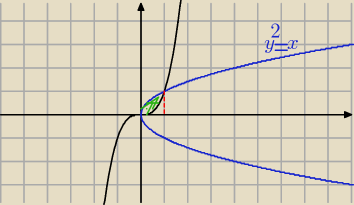
Mila: y²=x y=x³ y=(y²)³ y=y⁶ y⁶−y=0 y(y⁵−1)=0 y=0 lub y=1 x=0 lub x=1 granice całkowania

	2		1		5
P=0∫1(√x−x3)dx=[		x3/2−		x4]01=
	3		4		12

Bart: Dzięki, mi trochę inaczej wyszło aczkolwiek podobnie.

Mateusz: Oblicz pole obszaru ograniczonego krzywymi: y²=8*x 2*x − 3*y + 8=0