Całka w obszarze telo: Wyznaczyć całkę: ∫∫_a (x+1)dxdy gdzie A jest obszarem w R² ograniczonym krzywymi y²=2x, x+y=4, x+y=12 Czy ta całka jest równa: ∫₀⁸(∫_4−x^√2x (x+1) dy)dx + ∫₈¹⁸(∫_−√2x^12−x (x+1) dy)dx (Przepraszam za wygląd zapisu, pierwsza całka: x ∊ <0; 8>, y ∊ <4−x; √2x>, druga całka: x ∊ <8; 18>, y ∊ <−√2x; 12−x>)

Krzysiek: wszystko ok, poza pierwszą całką x∊[2,8]

telo: A no tak, przepraszam i dziękuję

Basia: (4−x)² = 2x 16 − 8x + x² = 2x x² − 10x + 16 = 0 Δ = 100 − 64 = 36

	10−6
x1 =		= 2
	2

	10+6
x2 =		= 8
	2

y₁ = 2 y₂ = −4 A(2;2) B(8;−4) (12−x)² = 2x 144 − 24x + x² = 2x x² − 26x + 144 = 0 Δ = 676 − 576 = 100

	26−10
x1 =		= 8
	2

	26+10
x2 =		= 18
	2

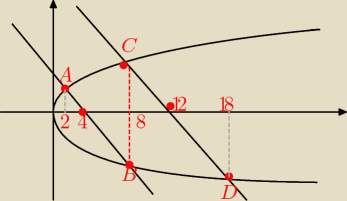
y₁ = 4 y₂ = −6 C(8;4) D(18;−6) druga całka w porządku; ale pierwsza nie (patrz rysunek) − dolna granica to 2