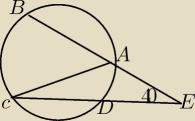
Geometria z gwiazdka czyli "Mozg rozjebany" Uczen Pani Białek: Dlugosc cieciw AB , BC , CD są rowne ∡E =40stopni. Oblicz miare kąta ACD

Uczen Pani Białek: Odkrece gaz, nie zapuka nikt na czas...

ICSP: 20

ICSP: Szukaj trójkąta równobocznego

ICSP: jednak nie Czekaj chwilke

Uczen Pani Białek: No własnie tez tak myslalem, lecz nie ma lekko ; d

Skipper:

Uczen Pani Białek: Cos wiecej ? Jakies wytlumaczenie? Bylbym wdzieczny.

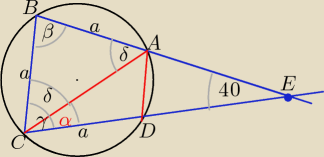
Bogdan: Rozwiązanie, czyli wyznaczenie wartości α stanie się łatwe po odpowiedzi z uzasadnieniem na pytania: 1. czy czworokąt ABCD jest trapezem równoramiennym o podstawach AD i BC ? 2. czy trójkąt EBC jest równoramienny ?

pigor: ... niech |∡|ACD|=x= ? − szukana miara kąta , to także |∡|ABD|=|∡|ACD|=x − jako miary kątów wpisanych opartych na tym samym łuku odpowiadającym cięciwie AD , ponadto |∡|ACB|=|∡|ADB| =|∡|BDC=α − jako ,że dwa pierwsze kąty są wpisane oparte na tym samym łuku odpowiadającym cięciwie AB , a drugi i trzeci kąt, jako katy przy podstawie trójkąta równoramiennego BDC, zatem z sumy kątów ΔBCE i warunku dla czworokąta ABCD wpisanego w okrąg mamy np. układ równań : (α+x)+(α+x)+40^o=180^o i (a+x)+(α+α)=180^o ⇔ ⇔ 2α+2x=140^o i 3α+x=180^o ⇔ α=70^o−x i x=18)^o−3α ⇒ x=180^o−3(70−x) ⇔ ⇔ x=−30^o+3x ⇔ 30^o=2x ⇔ x=15^o=|∡ACD| − szukana miara ∡|ACD| . ...

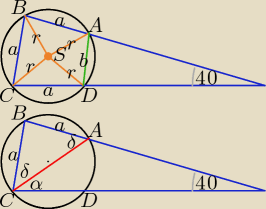
Bogdan: Myślę, że tak jest najprościej:

	180o − 40o
Trójkąty ABS, BCS i CDS są przystające, więc |∡ABC| = |∡BCD| =		= 70o,
	2

α + δ = 70^o

	180o − 70o
W trójkącie równoramiennym ABC: δ =		= 55o ⇒ α = 70o − 55o = 15o
	2