znajdź pierwiastki równania Kuba: Znajdź pierwiastki równania x⁵ − 32 =0

Ajtek: x⁵−32=0 x⁵=32 / ⁵√ x=....

Saizou : x⁵−32=0 x⁵=32 x=2

Kuba: nie dopisałem, że wyjaśnienie ma być na liczbach zespolonych ;x studia

ICSP: ⁵√32 i jedziesz ze wzoru De moivier'a

Kuba: Mógłbyś mi pokazać jak to zrobić? Proszę.

ICSP: Przecież wszystko jest łądnie opisane : http://pl.wikipedia.org/wiki/Wz%C3%B3r_de_Moivre'a

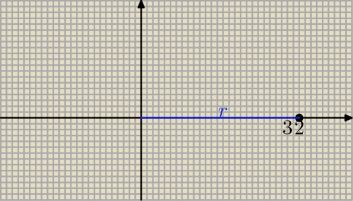
Mila: z=32+i*0 |z|=32 Φ=0 postać trygonometryczna liczby podpierwiastkowej z = 32*(cos 0 + i sin 0)

	0+2kπ		0+2kπ
5√z=5√|32|(cos		+isin		dla k∊{0,1,2,3,4}
	5		5

z₁=2*(cos 0 + i sin 0)=2

	2π		2π
z2=2*(cos		+isin		)=
	5		5

cos 72 ⁰ i sin72⁰ znajdź w tablicach ( jest wartość dokładna)

	4π		4π
z3=2*(cos		+isin		) dokończ
	5		5