Równania trygonometryczne Piterek1994: Rozwiązywałem sobie równania z pewnego zadania i trafiłem na takie coś: sin⁷x * cos⁷x =

	1
		i nie mam pomysłu. Przykład nawet mi wydaję się banalny, ale jednak nie mam pomysłu
	128

. Więc może ktoś podpowie jak to zrobić, albo chociaż jak zacząć? Z góry dzięki Ps. W razie pomocy proszę o dokładne wytłumaczenie sposobu rozwiązania najlepiej kroczek po kroczku

Bogdan: Podpowiedź: (sinx cosx)⁷ = 2⁻⁷ 2sinx cosx = sin(2x)

Bogdan: Kroczki sam jednak musisz stawiać

Ajtek:

	1
sinx7*cosx7=
	27

	1
(sinx*cosx)7=		/7√
	27

	1
sinx*cosx=		/*2
	2

2sinx*cosx=1 sin2x=1 dasz radę dalej?

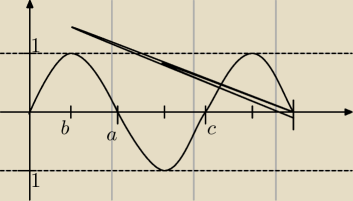
Piterek1994: Na rysunku fragment funkcji y=sin(2x)

	π
a=
	2

	π
b=
	4

c=π Tak siedziałem sobie i robiłem aż odświeżyłem stronę i zobaczyłem Twoją odpowiedź Ajtek. Doszedłem do tego, ale teraz funkcja y=sin(2x) przy wartości 1 przyjmuje w mierze kątowej

	π		π
		. Więc rozwiązaniem tego powinno być x=		+ 2kπ jednak w odpowiedziach jest x=
	4		4

	π
		+ kπ, więc gdzie zrobiłem błąd?
	4

Przepraszam za moją niewiedzę, ale ledwo ją sobie zaczęliśmy w klasie 2, a nasza pani ponieważ jestem na profilu z rozszerzoną matematyką uważa że powinniśmy już wszystko umieć i przeskoczyło jej się kilka lekcji i ze wstępu do trygonometrii jestem już przy równaniach i nierównościach.

Piterek1994: Sorki za jakość rysunku, ale już nie ogarniam cały dzień przy książkach

Bogdan: (sinx cosx)⁷ = (2⁻¹)⁷ sinx cosx = 2⁻¹ ⇒ 2sinx cosx = 1 ⇒ sin2x = 1

	π		1		π
2x =		+ k*2π /*		⇒ x =		+ k*π
	2		2		4

Mila:

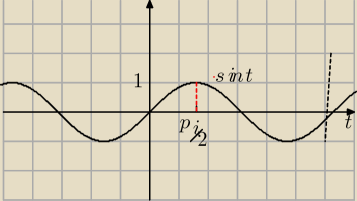
	π
sint =1 dla t=		rozważamy przedział <0,2π>
	2

sin2x=1⇔

	π
2x=		+2kπ /:2⇔
	2

	π
x=		+kπ
	4

Piterek1994: Ok to ma sens tylko Mila czy możesz mi wytłumaczyć dlaczego przy funkcji y=sin2x wykorzystujesz rysunek funkcji y= sinx? Jak to mi wytłumaczysz to już wszystko będzie dla mnie jasne.

Mila: Dla sinx ( ja nawet napisałam sin t) znamy wykres i wartości w przedziale <0;2π>. Możesz zrobić podstawienie 2x=t

Bogdan: a po co to? przecież rozwiązanie już podałem.

Piterek1994: Ok dzięki za pomoc