Proszę o pomoc(MAT ZR) bartolinos: ZAD1.Oblicz pole trójkąta ABC znając b=√3 −1 , c=3− √3, β=30st. Zad 2. Liczba 1 jest pierwiastkiem wielomianu W(x). Wyznacz resztę z dzielenia tego wielomianu przez P(x)=x² − 3x+2 jeśli wiadomo, że W(x) z dzielenia przez x−2 daje resztę −7

@Basia: Podpowiadam

bartolinos: Będę wdzięczny

@Basia: P(x) = x²−3x+2 Δ=9−4*1*2 = 1 √Δ=1

	3−1
x1 =		= 1
	2

	3+1
x2 =		= 2
	2

P(x) = (x−1)(x−2) P(1) = 0 P(2)=0 W(x) = P(x)*Q(x) + R(x) W(1)=P(1)*Q(1) + R(x) = 0*Q(1) + R(1) = 0+R(1) = R(1) ale W(1) = 0 (bo 1 jest jego pierwiastkiem) czyli R(1)=0 z treści wynika, że R(2)=−7 to zadanie daje się rozwiązać tylko wtedy jeżeli wiadomo, że W(x) jest wielomianem 3 stopnia wtedy R(x) = ax+b R(1) = 0 a*1+b=0 a+b=0 −−−−−−−−−−−−−−−−− R(2)=−7 a*2+b = −7 2a+b = −7 −−−−−−−−−−−−−−−− rozwiązujemy układ równań dla W(x) stopnia wyższego niż 3 zadanie jest nierozwiązywalne (za mało danych)

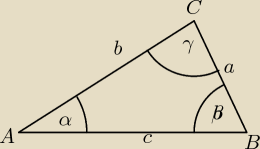
@Basia: b=√3−1 c=3−√3 β=30 z tw.sinusów ^sinβ_b = ^sinγ_c

sin30		sinγ
	=
√3−1		3−√3

	12*(3−√3)
sinγ =
	√3−1

	3−√3
sinγ=
	2(√3−1)

	√3(√3−1)
sinγ=
	2(√3−1)

	√3
sinγ=
	2

γ=60 α+β+γ = 180 α+30+60=180 α=90 i w takim razie

	b*c		(√3−1)(3−√3)
P=		=
	2		2

	3√3−3−3+√3		4√3−6
P=		=		= 2√3−3
	2		2

bartolinos: Dzięki. Bardzo mi pomogłaś