wektory pati: Punkty A(−3,−1), B(1,2), C(2,5) są kolejnymi wierzchołkami równoległoboku ABCD. a) Oblicz współrzędne wierzchołka D. b) Oblicz współrzędne punktu S przecięcia się przekątnych. c) Oblicz długości przekątnych równoległoboku. Bardzo prosze o pomoc!

TOmek: a) AB jest równoległe do CD wyznaczasz wzór prostej AB. Prosta CD bedzie miała ten sam wspołczynnik kierunkowy (y_CD=ax+b) Otrzymamy prawie cały wzór prostej CD (y_CD=ax+b). Wystarczy ,ze postawimy punkt C do wzoru prostej CD a otrzymamy jest całkowity kształt. −czyli mamy juz wzór na prostą CD I po tym można zastosować pewien manewr; przyrównujemy długosci odcinków |BC|=|AD| gdzie (x,y_CD) => (x,ax+b) −> wiadomo ,ze tutaj wstawiamy to co nam wyjdzie)

Bogdan: Nie potrzeba TOmek wyznaczać równanie prostej. A(−3, −1), B(1, 2), C(2, 5), D(x_D, y_D),

	−3 + 2		1
S(		, −1 + 52) = (−		, 2)
	2		2

	1
1 + xD = 2*(−		) ⇒ xD = ...
	2

2 + y_D = 2*2 ⇒ y_D = ...

TOmek: wybrałem trudniejszy sposob, ale poprawy

Bogdan: Po kiego diabła?, jak mówi Basia trudniejszy sposób, a przez to bardziej czasochłonny i bardziej podatny na zrobienie błędu. Sprawdziany, egzaminy mają ograniczony czas i trzeba wybierać proste rozwiązania. To, jak jazda z Zakopanego do Krakowa przez Gdańsk. Kto chce, niech tak sobie jeździ, ale polecać takiej wydłużonej drogi nie powinno się. Pozdrawiam

Bogdan: Przy okazji tego zadania: A(x_A, y_A), B(x_B, y_B), środek S(x_S, y_S)

xA + xB
	= xS ⇒ xA + xB = 2xS ⇒ xB = 2xS − xA
2

yA + yB
	= yS ⇒ yA + yB = 2yS ⇒ yB = 2yS − yA
2

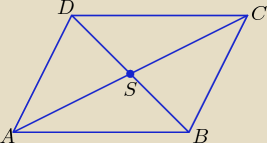
Gustlik: Bogdan, nie 100 a 1000 % racji, "jazda z Zakopanego do Krakowa przez Gdańsk" − jakbym czytał swoje posty. Wyjąłeś mi to z ust, a raczej z klawiatury ! Mozna jeszcze prościej − wektorami. Punkty A(−3,−1), B(1,2), C(2,5) są kolejnymi wierzchołkami równoległoboku ABCD. a) Oblicz współrzędne wierzchołka D. b) Oblicz współrzędne punktu S przecięcia się przekątnych. c) Oblicz długości przekątnych równoległoboku. Bardzo prosze o pomoc! 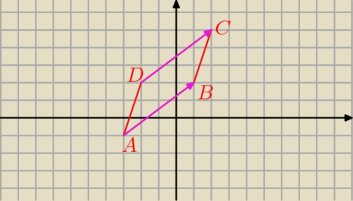ad a) wektorami. AB^→=[1−(−3), 2−(−1)]=[4, 3] DC^→=AB^→=[4, 3] DC^→=C−D=[2−x, 5−y] 2−x=4 −x=2 x=−2 5−y=3 −y=−2 y=2 D=(−2, 2)

Bogdan: Witaj Gustliku , nie pokazywałem wektorami, bo ich obecni uczniowie nie znają, pokazałem dostępny dla nich sposób, zresztą w tym przypadku nie mniej prosty.

Gustlik: A(−3,−1), B(1,2), C(2,5), D=(−2, 2) ad b)

	−3+2		−1+5		1
S=(		,		)=(−		, 2)
	2		2		2

ad c) wektorami AC^→=[2−(−3), 5−(−1)]=[5, 6] |AC|=√5²+6²=√25+36=√61 BD^→=[−2−1, 2−2]=[−3, 0] |BD|=√(−3)²+0²=3

Gustlik: Bogdan, tym bardziej trzeba je pokazywać ! Ten program to totalna KASZANA ! Wektory sa proste jak konstrukcja młotka, każdy je zrozumie, a to podstawa GEOMETRII ANALITYCZNEJ. Co jest trudnego we wzorze AB^→=[x_B−x_A, y_B−y_A] ? Samo odejmowanie, zcasem wyjdzie tez dodawanie, VI−klasista by to zrozumiał, jakby mu w miarę dobrze wytłumaczyć. Ten wzór jest też w karcie maturalnej. Pozdrawiam.

Gustlik: A propos programu − wczoraj przyszedł do mnie uczeń z I klasy LO i przyniósł książkę z fizyki. Zastanawiałem się czy to książka do fizyki czy może do przyrody dla szkoły podstawowej. TOTALNE DNO ! Jak tak dalej pójdzie to nauka fizyki będzie się ograniczała do takich sformułowań: Żarówka świeci. Słońce świeci. Prąd płynie. Żelazko grzeje. Silnik się kręci. Samochód jedzie. Ale wyjaśnienia, dlaczego żarówka świeci, czy samochód jedzie NIE BĘDZIE. Rany boskie, co oni robią z tym programem? Ja w podstawówce mialem lepiej opracoane podręczniki, niż dzisiaj mają w liceum. Dodam, że jeszcze 3 lata temu w gimnazjum był bardziej ambitny program z ficyki − rozwiązywano zadania, takie na myślenie. A dzisiaj − pełno kolorowych obrazków, trochę pisaniny, a przykładów obliczeniowych jak na lekarstwo − ta książka przypomina bardziej książki dla dzieci w wieku przedszkolnym niż książke z fizyki dla LO.