rozwiąż równianie. Gocha: niby banalne, ale ja nie ogarniam jak to zrobić. mam rozwiązać nierówność x² ≤ 7x Proszę o pomoc i wyjaśnienie czemu tak, a nie inaczej trzeba zrobić.

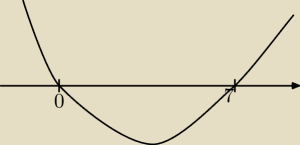
Patronus: Nie możesz tu podzielić przez x, bo nie wiesz czy jest dodatni czy ujemny i czy zmienić znak czy nie. Zatem: x² − 7x ≤ 0 x(x−7)≤0 I z rysunku wynika, że x∊<0;7>

Gocha: Dziękuję bardzo Mam straszną babeczkę od matmy, a tak to pracę domową mam z głowy i zero stresu, że nie ogarniam Jestem baaardzo wdzięczna.

ZKS: Patronus o tyle nawet nie chodzi czy znamy czy nie znamy znaku ale przecież x = 0 jest rozwiązaniem a przez 0 dzielić nie można.

PW: Ale można pomyśleć tak: lewa strona równania jest dodatnia dla dowolnego x≠0, a więc żadna liczba ujemna nie jest pierwiastkiem (bo wtedy prawa strona jest ujemna). Wobec tego szukajmy pierwiastków wśród liczb dodatnich, a wtedy można podzielić przez x nie zmieniając nierówności na przeciwną. Dostajemy w ten sposób nierówność x≤7 dla x>0, której rozwiązaniem jest zbiór (0,7>. To razem z uwagą ZKS daje pełne rozwiązanie: zbiór <0,7>. Okazało sie, że można rozwiązać to zadanie bez znajomości przebiegu funkcji kwadratowej.

pigor: ... tak, o funkcji kwadratowej nie musimy tu nic wiedzieć bo można np. tak : x²≤ 7x ⇔ x²−7x≤ 0 ⇔ x(x−7)≤ 0 ⇔ (x≥0 ∧ x−7≤0) ∨ (x≤0 ∧ x−7≥0) ⇔ ⇔ (x≥0 ∧ x≤7) ∨ (x≤0 ∧ x≥7) ⇔ 0≤ x ≤7 ∨ x∊∅ ⇔ 0≤ x ≤7 ⇔ x∊[0;7] .