obliczanie powierzchni przekroju
patrycja: Jak obliczyc powierzchnie przekroju szescianu, zawierajacego srodki sasiednich kraawedzi
podstaw z wierzcholkiem najbardziej oddalonym od tego odcinka. Bardzo prosze o dokladna pomoc.
Sam przekroj narysowalam, ale nad powierzchnia mecze się bardzo dlugo.
6 wrz 12:08
Artur_z_miasta_Neptuna:
narysuj ten szcześcian i jak wygląda ten przekrój
6 wrz 12:10
anmario:
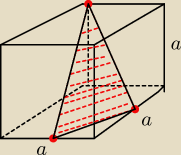
Przekrojem jest trójkąt równoramienny, oblicz długość jego podstawy, (z tw Pitagorasa) wysokość
(również z Pitagorasa, ale do wyliczenia wysokości potrzebna jest długość ramienia tego
trójkąta, więc najpierw musisz tą długość wyliczyć, z czego? − ano z Pitagorasa)

6 wrz 12:32
pigor: ... rozumiem, że mamy długość
a − boku sześcianu , no to niech
r,h= ? − długości
odpowiednio ramienia i wysokości przekroju , czyli trójkąta równoramiennego o podstawie
p=12a√2 na rys. powyżej , to
| | 1 | |
Sp= 12ph= 12*12a√2*h= |
| a√2h= ? −szukane pole przekroju , |
| | 4 | |
przy czym :
r2=a
2+
14a
2+a
2=
84a
2+
14a
2=
94a2 , więc
h
2=r
2−
14p
2=
94a
2−
14*
24a
2=
188a
2−
18a
2=
| | a√17 | |
= 178a2 ⇒ h= |
| , zatem |
| | 2√2 | |
| | 1 | | a√17 | |
Sp= |
| a√2 * |
| = 18a2√17 . ...  |
| | 4 | | 2√2 | |
6 wrz 14:12
Atanazy:
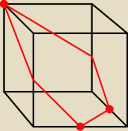
Zastanawiam się, czy ten przekrój nie powinien wyglądać tak, jak wyżej ?
Mogę się mylić, co więcej− to może być ten sam przekrój. Jeśli nie, to ciekaw jestem... Coś się
zmieni przy rozwiązywaniu zadania ?
6 wrz 18:56
patrycja: Tez mialaam taki obrazek jak podal Atanazy, wiec czy sposob pigor jest dobry ? Z gory dziekujee
za pomoc

!
6 wrz 19:37
Aga1.: Trójkąt na rysunku nie jest żadnym przekrojem, więc i obliczenia nie do tego zadania.
6 wrz 20:11
patrycja: proszę o pomoc glowie sie i glowie i kazdym sposobem wychodzi mi zle
6 wrz 20:45
Aga1.: Masz odpowiedź?
6 wrz 20:46
patrycja: niestety nie..
6 wrz 20:48
patrycja: jest jakas mozliwosc wyniku jesli milion obliczej pozniej a caly czas wynosi 0

6 wrz 22:29
anmario:
Rzeczywiście, kompletna bzdura ten mój przekrój. Szkoda, że nie mam teraz czasu zastanowić się
nad tym, mogę wrócić do tego zadania dopiero jutro wieczorem. Myślę, że do tego czasu ktoś już
zaproponuje właściwe rozwiązanie. Jeżeli nie chwycę za piłę i zniszczę jakiś drewniany
sześcianik, ale na teraz sądzę, że ten przekrój będzie chyba wyglądał tak jak namalował
Atanazy, cóż kiedy szybkiego sposobu na obliczenie jego pola nie widzę.
6 wrz 23:05
pigor: ... no cóż i ja się złapałem na taki bzdurny przekrój . ...

6 wrz 23:21
Mila:
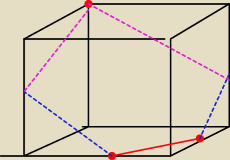
6 wrz 23:24
asdf:
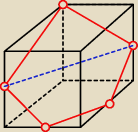
przeciąć to można (niebieska linia) i obliczyć: trapez + trójkąt
6 wrz 23:28
patrycja: juz chyba mam dziękuję serdecznie

7 wrz 00:23
asdf:
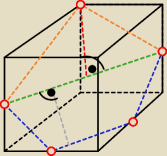 zielona = U{a√2
zielona = U{a√2
7 wrz 00:24
anmario:
Niestety nie asdf, przecież niebieskie odcinki nie są sobie równe, będą równe tylko wtedy
kiedy cięcie będzie od wierzchołka do wierzchołka
7 wrz 00:46
anmario:
A Ty, jak masz to rozwiązanie Patrycja to pochwal się może, bardzo ciekawe zadanie.
7 wrz 00:48
asdf: @anmario
To jest sześcian
7 wrz 00:51
asdf: I wszystkie są w połowie..
7 wrz 00:51
anmario:
Ja próbowałem coś w tym rodzaju:
h
1 − wysokość trójkąta: nieznana
h
2 − wysokość trapezu: nieznana
a − dłuższa podstawa trapezu i jednocześnie podstawa trójkąta: łatwa do obliczenia, znana
b − krótsza podstawa trapezu: łatwa do obliczenia, znana
H = h
1 + h
2: łatwa do obliczenia, znana
| | a+b | | a | | a | | b | | a | |
P = |
| * h2 + |
| * h1 = |
| * (h1 + h2) + |
| * h2 = |
| * H + |
| | 2 | | 2 | | 2 | | 2 | | 2 | |
| | b | | H | | a | | b | | H | | a | |
|
| * h2 * |
| = |
| * H + |
| * h2 * |
| = |
| * H + |
| | 2 | | H | | 2 | | 2 | | h1 + h2 | | 2 | |
| | b | | H | | a | | b | | H | |
|
| * |
| = |
| * H + |
| * |
| |
| | 2 | | | | 2 | | 2 | | | |
I teraz próbuję znaleźć związek między h
1 a h
2, niestety ani z Talesa ani z podobieństwa nic
sensownego nie wychodzi
7 wrz 00:53
anmario:
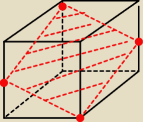
Tak są w połowie
Asdf, w przypadku z zadania w połowie w związku z tym być nie mogą
7 wrz 00:59
asdf: Nie rozumiem Ciebie

7 wrz 01:02
asdf: P.S Chyba zły rysunek
7 wrz 01:05
anmario:
Zauważ, że łatwo obliczyć H, mam na myśli sumę wysokości trapezu i trójkąta, pełne rozwiązanie
podał pigor. Jeżeli nie widzisz tego tak jak ja, to po prostu zsumuj długości wysokości,
które wyliczyłeś i zastanów się dlaczego ta suma nie jest taka sama jak całe H,
7 wrz 01:09
anmario:
No wreszcie chyba mam, jednak z podobieństwa. Nie mam, niestety już poweru by dokładnie
sprawdzić obliczenia a tym bardziej na ich zaprezentowanie

7 wrz 02:42
asdf: @
anmario I jak? wstałeś

Co ty chcesz liczyć z podobieństwa, skoro wszystkie ściany są
takie same?
7 wrz 11:17
pigor: ....

coś mi sie wydaje, że
anmario niemało namieszał w głowach (przede wszystkim mnie),
dlatego jeszcze raz przeczytałem kilka razy treść tego zadania , a raczej "wczytałem się" w
pytanie autorki postu i stwierdzam, że chodzi jej po prostu o
sześciokąt foremny o boku
x taki, że x
2=a
2+
14a
2=
54a
2, a wtedy
S=6*
14x
2√3=
32*
54a
2√3=
158a2√3 − szukane pole . ...

7 wrz 12:43
Aga1.:
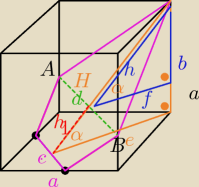
| | 1 | | 1 | |
P{pięciokąta}=Ptrójkąta+Ptrapezu= |
| d*h+ |
| (d+c)*h1 |
| | 2 | | 2 | |
Punkty A i B nie muszą być środkami krawędzi bocznych ( a jeśli są to trzeba to udowodnić)
7 wrz 12:45
asdf: Dzięki Aga1, teraz rozumiem o co chodziło anmario...
7 wrz 12:52
pigor: ... choć mogę się mylić, bo autorka postu pisze coś o wierzchołku sześcianu

, dlatego to
nie wygląda mi na przemyślaną, czyli jednoznaczną treść zadania , nie mówiąc o tym, że np.
nie wiemy co jest dane ( długość krawędzi sami sobie przyjęliśmy za daną

) . ...

7 wrz 13:02
Mila: Patrycja,czy już obliczyłaś pole tego przekroju? Ja mogę policzyć po 22. Teraz wychodzę.
Odpowiedz, czy liczyć.
7 wrz 16:09
anmario:
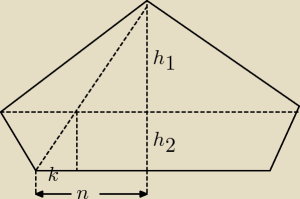
H = h
1 + h
2
I układ trzech równań z trzema niewiadomymi, który pozwala wyliczyć h
1 i h
2:
h
1+h
2 = H
7 wrz 16:14
anmario:
Dla porządku powinienem dodać, że niewiadome to h
1, h
2 i k, cała reszta da się prosto
wyliczyć, być może powinienem dodać i więcej jeszcze, na przykład obliczyć to pole, ale to
szczegół już a czas mnie goni, sorki

7 wrz 16:18
Aga1.: d=a
√2
H
2=e
2+a
2⇒H= ...dokończ
| | f | | f | |
cosα= |
| ⇒h= |
| =.. dokończ |
| | h | | cosα | |
h
1=H−h.
Podstaw do wzoru na pole.
7 wrz 16:27
anmario:
| | 1 | |
f = |
| d  |
| | 2 | |
Nie za bardzo
7 wrz 16:39
anmario: A nie, oczywiście, że tak
7 wrz 16:42
Bogdan:
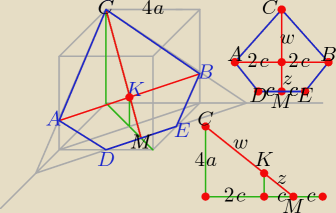
Dla wygody obliczeń przyjmuję długość krawędzi sześcianu b = 4a.
Długość przekątnej każdej ściany jest więc równa 4a
√2 = 4c ⇒ c = a
√2 i 3c = 3a
√2
Na podstawie twierdzenia Pitagorasa (prawy dolny rysunek):
w + z =
√16a2 + 9c2 =
√16a2 + 18a2 = a
√34
| | 3c | | c | |
Z podobieństwa trójkątów (ten sam rysunek): |
| = |
| ⇒ w = 2z |
| | w + z | | z | |
| | 1 | | 2 | |
w + z = 2z + z = 3z = a√34 ⇒ z = |
| a√34 i w = |
| a√34 |
| | 3 | | 3 | |
| | 2 | |
|AB| = 4c = 4a√2, |KC| = w = |
| a√34, |
| | 3 | |
| | 1 | |
|DE| = 2c = 2a√2, |KM| = z = |
| a√34 |
| | 3 | |
P − pole pięciokąta ADEBC, P
1 − pole trójkąta ABC, P
2 − pole trapezu ADEB
P = P
1 + P
2
| | 1 | | 1 | | 2 | | 8 | |
P1 = |
| |AB|*|KC| = |
| * 4a√2 * |
| a√34 = |
| a2√17 |
| | 2 | | 2 | | 3 | | 3 | |
| | 1 | | 1 | | 1 | |
P2 = |
| |KM|*(|AB| + |DE|) = |
| * |
| a√34 * 6a√2 = 2a2√17 |
| | 2 | | 2 | | 3 | |
| | 8 | | 14 | | 7 | |
P = |
| a2√17 + 2a2√17 = |
| a2√17 ⇒ P = |
| b2√17 ≈ 1,2b2 |
| | 3 | | 3 | | 24 | |

8 wrz 01:48
Aga1.: Tyle wyszło
| | (3a√2 | | 18a2 | | √34a | |
H=√ |
| )2+a2=√ |
| +a2= |
| |
| | 4 | | 16 | | 4 | |
| | √34a | | √34a | | √34a | |
h1= |
| − |
| = |
| |
| | 4 | | 6 | | 12 | |
| | 1 | | √34a | | 1 | | a√2 | | √34a | |
P= |
| *a√2* |
| + |
| (a√2+ |
| )* |
| |
| | 2 | | 6 | | 2 | | 2 | | 12 | |
| | a2√68 | | a√34 | | 3a√2 | | 2a2√17 | | 6a2√17 | |
P= |
| + |
| * |
| = |
| + |
| = |
| | 12 | | 24 | | 2 | | 12 | | 24 | |
| 4a2√17 | | 3a2√17 | | 7a2√17 | | 7 | |
| + |
| = |
| = |
| a2√17 |
| 24 | | 24 | | 24 | | 24 | |
8 wrz 09:56
 Przekrojem jest trójkąt równoramienny, oblicz długość jego podstawy, (z tw Pitagorasa) wysokość
(również z Pitagorasa, ale do wyliczenia wysokości potrzebna jest długość ramienia tego
trójkąta, więc najpierw musisz tą długość wyliczyć, z czego? − ano z Pitagorasa)
Przekrojem jest trójkąt równoramienny, oblicz długość jego podstawy, (z tw Pitagorasa) wysokość
(również z Pitagorasa, ale do wyliczenia wysokości potrzebna jest długość ramienia tego
trójkąta, więc najpierw musisz tą długość wyliczyć, z czego? − ano z Pitagorasa) 

 Zastanawiam się, czy ten przekrój nie powinien wyglądać tak, jak wyżej ?
Mogę się mylić, co więcej− to może być ten sam przekrój. Jeśli nie, to ciekaw jestem... Coś się
zmieni przy rozwiązywaniu zadania ?
Zastanawiam się, czy ten przekrój nie powinien wyglądać tak, jak wyżej ?
Mogę się mylić, co więcej− to może być ten sam przekrój. Jeśli nie, to ciekaw jestem... Coś się
zmieni przy rozwiązywaniu zadania ?
 !
!



 przeciąć to można (niebieska linia) i obliczyć: trapez + trójkąt
przeciąć to można (niebieska linia) i obliczyć: trapez + trójkąt


 Tak są w połowie Asdf, w przypadku z zadania w połowie w związku z tym być nie mogą
Tak są w połowie Asdf, w przypadku z zadania w połowie w związku z tym być nie mogą


 Co ty chcesz liczyć z podobieństwa, skoro wszystkie ściany są
takie same?
Co ty chcesz liczyć z podobieństwa, skoro wszystkie ściany są
takie same?
 coś mi sie wydaje, że anmario niemało namieszał w głowach (przede wszystkim mnie),
dlatego jeszcze raz przeczytałem kilka razy treść tego zadania , a raczej "wczytałem się" w
pytanie autorki postu i stwierdzam, że chodzi jej po prostu o sześciokąt foremny o boku
x taki, że x2=a2+14a2= 54a2, a wtedy
S=6*14x2√3= 32*54a2√3= 158a2√3 − szukane pole . ...
coś mi sie wydaje, że anmario niemało namieszał w głowach (przede wszystkim mnie),
dlatego jeszcze raz przeczytałem kilka razy treść tego zadania , a raczej "wczytałem się" w
pytanie autorki postu i stwierdzam, że chodzi jej po prostu o sześciokąt foremny o boku
x taki, że x2=a2+14a2= 54a2, a wtedy
S=6*14x2√3= 32*54a2√3= 158a2√3 − szukane pole . ... 

 , dlatego to
nie wygląda mi na przemyślaną, czyli jednoznaczną treść zadania , nie mówiąc o tym, że np.
nie wiemy co jest dane ( długość krawędzi sami sobie przyjęliśmy za daną
, dlatego to
nie wygląda mi na przemyślaną, czyli jednoznaczną treść zadania , nie mówiąc o tym, że np.
nie wiemy co jest dane ( długość krawędzi sami sobie przyjęliśmy za daną  ) . ...
) . ... 
 H = h1 + h2
I układ trzech równań z trzema niewiadomymi, który pozwala wyliczyć h1 i h2:
H = h1 + h2
I układ trzech równań z trzema niewiadomymi, który pozwala wyliczyć h1 i h2:


 Dla wygody obliczeń przyjmuję długość krawędzi sześcianu b = 4a.
Długość przekątnej każdej ściany jest więc równa 4a√2 = 4c ⇒ c = a√2 i 3c = 3a√2
Na podstawie twierdzenia Pitagorasa (prawy dolny rysunek):
w + z = √16a2 + 9c2 = √16a2 + 18a2 = a√34
Dla wygody obliczeń przyjmuję długość krawędzi sześcianu b = 4a.
Długość przekątnej każdej ściany jest więc równa 4a√2 = 4c ⇒ c = a√2 i 3c = 3a√2
Na podstawie twierdzenia Pitagorasa (prawy dolny rysunek):
w + z = √16a2 + 9c2 = √16a2 + 18a2 = a√34
