namniejsza najwieksza war funkcji
michal: mam tu wyznaczyc naJwieksza i najmniejsza wartosc funkcji:
f(x)= x4+6x3+4x2+1
na przedziale [−2,0]
nie wiem kompletnie co jak robic po kolei?
moze ktos mi pokazac jak sie to rozwiazuje ?
prosze..
5 wrz 22:06
wojtek: podstawiasz za x najwiąkszą wartość funkcji w przedziale czyli 0
i tez podstawiasz za x najniejsza wartość funkcji czyli −2
5 wrz 22:08
wojtek: czyli największa wartość funkcji to y=1
a najmniejsza juz sam policz

5 wrz 22:10
wojtek: najmniejsza wartość funkcji to tez 1 bo y= (−2)4 +6(−2)3 + 4(−2)2 +1 = 16−32+16+1 =1
5 wrz 22:15
wojtek: rozumiesz juz ?
5 wrz 22:15
Maslanek: f'(x)=4x3+18x2+8x
f'(x)=0 ⇔ 2x(2x2+9x+4)=0
No i trzeba zbadać znaki f'(x) w otoczeniu punktów.
5 wrz 22:15
Maslanek: Dla kontrprzykładu f(−1)=1−6+4+1=0.
Wojtuś, mniejsze masz z miejsca.

5 wrz 22:16
wojtek: masz racje sorry pomyłka

to jak powinno byc dla x = −2 ?
5 wrz 22:21
wojtek: dla x=−2 jest −11
5 wrz 22:23
Aga1.: Musisz policzyć ekstremum funkcji .
5 wrz 22:25
michal: tak

dziekuje
5 wrz 22:32
Mila:
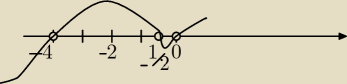
Badam kiedy pochodna jest dodatnia.
4x
3+18x
2+8x>0⇔
2x(2x
2+9x+4)>0⇔
Δ=49
miejsca zerowe wielomianu, x=0 lub x
1=−4 lub x
2=−0,5
funkcja nie jest monotoniczna w przedziale [−2;0] bo pochodna zeruje się w x=−0,5 i zmienia
znak.
| | 1 | |
f(x) ma ekstremum w x=− |
| i jest to maksimum. |
| | 2 | |
| | 1 | |
f(− |
| ) to będzie wartość największa . |
| | 2 | |
| | 1 | |
f(x) rośnie w przedziale (−4, − |
| ) |
| | 2 | |
Najmniejsza wartość dla x=−2 oblicz te wartości
5 wrz 22:43


 to jak powinno byc dla x = −2 ?
to jak powinno byc dla x = −2 ?
 dziekuje
dziekuje
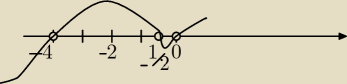 Badam kiedy pochodna jest dodatnia.
4x3+18x2+8x>0⇔
2x(2x2+9x+4)>0⇔
Δ=49
miejsca zerowe wielomianu, x=0 lub x1=−4 lub x2=−0,5
funkcja nie jest monotoniczna w przedziale [−2;0] bo pochodna zeruje się w x=−0,5 i zmienia
znak.
Badam kiedy pochodna jest dodatnia.
4x3+18x2+8x>0⇔
2x(2x2+9x+4)>0⇔
Δ=49
miejsca zerowe wielomianu, x=0 lub x1=−4 lub x2=−0,5
funkcja nie jest monotoniczna w przedziale [−2;0] bo pochodna zeruje się w x=−0,5 i zmienia
znak.