Trójkąt. Boki ... .. V.Abel: Pole trójkąta rozwartokątnego jest równe 8 j². Dwa boki trójkąta mają długości 4 i 5. Oblicz długość trzeciego boku. Który wzór na pole uwzględni rożne możliwości położenia boków ? ? ?

PW: Jest taki wzorek: pole trójkąta to połowa iloczynu dwóch boków i sinusa kata między nimi. No to sinus już masz. Pamiętając, że cosinus rozwartego jest ujemny, możesz na tej podstawie obliczyć cosinus. Mając cosinus obliczysz ten trzeci bok z twierdzenia cosinusów. Tyle, że to wszystko przy założeniu, że ten rozwarty kąt jest właśnie pomiędzy bokami o długościach 4 i 5. Jeżeli tak nie jest, to chyba pozostaje koszmar wzoru Herona.

ICSP: Nie lepiej ze wzoru Herona ?

Ajtek: Jaki koszmar Herona To bardzo przydatny wzorek do tego typu zadań .

PW: Za wcześnie się poddałem. Jeśli tak nie jest, czyli cosinus jest dodatni (równy 3/5), to trójkąt miałby trzeci bok równy √17, a więc nie jest rozwartokątny, bo ... V.Abel − wiesz dlaczego?

V.Abel: PW dlatego, że cosinus jest dodatni, czyli kąt nie jest rozwarty, tak? Czyli teraz Heronem, tak ?

Saizou :

	ah
wykorzystam wzór P+
	2

	5h
8=
	2

16=5h h=3,2 z tw. Pitagorasa mamy że 3,2²+a²=4² a²=16−10,24 a²=5,76 a=2,4 b=5−a=5−2,4=2,6 z tw. Pitagorasa (2,6)²+(3,2)²=c² c²=6,76+10,24 c²=17 c=√17

Saizou :

	ah
* P=
	2

PW: Do V.Abel Nie o to idzie. Po wyliczeniu sinusa możemy obliczyć cosinus (z jedynki trygonometrycznej) i otrzymamy dwie możliwości: albo cosinus jest ujemny czyli kąt rozwarty (koniec rozwiązania), albo dodatni, czyli tego rozwartego trzeba szukać między innymi bokami. Ale od razu sobie odpowiadamy: nie ma co szukać, trójkąt o bokach 4, 5 i √17 nie może być rozwartokątny, bo ... I o to pytałem.

Saizou : I jeśli 4 i 5 są przyprostokątnymi to przeciwprostokątna powinna być większa od c>√41 wtedy jest kąt rozwarty II jeśli 5 jest przeciwprostokątną to c>5 żeby był kąt rozwarty III jeśli 4 jest przeciwprostokątną to c>4 √17≈4,12 więc chyba może być czy coś źle rozumiem

V.Abel: PW : Ja podstawiłem do Tw. cosinusów boki 4,5,√17 i mi wyszedł cos na minusie, dlatego, wg mnie, taki Δ rozwarty być nie może. Czy o to Ci chodzi?

V.Abel: sorry, cos na plusie, dlatego nie jest rozwarty ** pardon

+-: Czemu tak wystraszyliście się "Herona " p= (9+x) /2 8=1/4*√(9+x)(9+x−10)(9+x−8)(9+x−2x)=1/4*√(9+x)(x−1)(1+x)(9−x)=1/4*√(9²−x²)(x²−1) 32²=81x²+81−x⁴+x² X⁴−82x²+1105=0 z²−82z+1105=0 Δ=2304 √Δ=48 Z1=17 z2=65 x1=√17 nie odpowiada warynkom zadania trójkąt ma być rozwartokątny x3=√65 Spełnia warunek trójkąt rozwartokątny Jak widać nie zawsze diabeł taki straszny jak się wydaje,

Mila: P_Δ=U[1}{2}*4*5*sinα=10sinα 10sinα=8

	4
sinα=
	5

	16		9
cos2α=1−		=
	25		25

	3
Cosα=U{3}[5} lub cosα=−
	5

	3
I) cosα=−		kąt między bokami o długości 4 i 5 jest rozwarty.
	5

	3
c2=42+52−2*4*5*(−		=65
	5

c=√65 II) kąt między bokami o długości 4 i 5 jest ostry

	3
c2=42+52−2*4*5*		=17
	5

c=√17<5 jeśli istnieje w tym trójkącie kąt rozwarty, to leży naprzeciw najdłuższego boku: Sprawdzam znak cos β 5²=√17²+4²−2*4*√17cosβ −8= −8√17cosβ

	8
cosβ=		>0 zatem kąt β jest ostry
	8√17

odp. c=√65

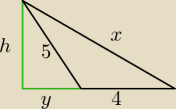
+-: Chyba prościej nie będzie, mozna w pamięci niech postawą będzie bok 4, wówczas h=2S/4=2*8/4=4 , (Trójkąt Pitagorasa) y=√5²−4²=3 Dalej z Pitagorasa mamy x=√h²+(y+4)²=√4²+7²=√65

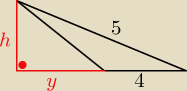
Basia: bardzo ładny i elegancji sposób , ale jeszcze trzeba rozważyć ten przypadek (doprowadzi do sprzeczności, ale z góry nie można tego założyć) też można tym sposobem h = 4 (y+4)²+h² = 5² (y+4)²+4² = 5² (y+4)² = 9 y+4 = 3 y = −1 sprzeczność czyli √65 jest jedynym rozwiązaniem

Aga1.: Licząc ze wzoru Herona nie trzeba rozważać dwóch przypadków , chociaż obliczenia trudniejsze.

+-: jeżeli już to co prawda oba ujemne (y+4)2 = 9 y1=−7 y2=−3

Basia: y+4 > 0 (jest długością) rozwiązanie y+4 = −3 można pominąć

PW: Do +−: No o to cały czas idzie: kto powie wyraźnie, dlaczego trójkąt o bokach 4, 5 i √17 nie jest rozwartokątny? A Herona nie lubię, bo jestem leniwy (podobno matematyka nauką ludzi leniwych).

Aga1.: Najdłuższy bok to √17 √17²>4²+5² jeśli taka nierówność jest prawdziwa, to trójkąt jest rozwartokątny . Drugi sposób obliczyć cosinus kąta α zawartego między bokami 4 i 5. Jeśli cosα<0 to α jest kątem rozwartym, a trójkąt jest rozwartokątny

Mila: PW− nie wiesz, czy sprawdzasz pomagających, jak to masz w zwyczaju?

anka: βγ