W kulę o promieniu R = wpisano walec, w którym stosunek promienia podstawy do w boni: W kulę o promieniu R = wpisano walec, w którym stosunek promienia podstawy do wysokości jest równy 3 : 4 . Oblicz pole powierzchni całkowitej i objętość walca

@Basia: Rysuję. To chwilę potrwa

pazio: ambitnie

imię lub nick: proste

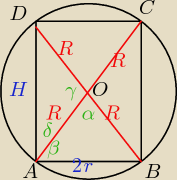
@Basia: γ=180−α δ=90−β ^r_H = ³₄ z tw. sinusów w △AOB mamy:

sinα		sinβ
	=
2r		R

2r*sinβ=R*sinα

	R*sinα
r=
	2sinβ

z tw.sinusów w △AOD mamy:

sin(180−α)		sin(90−β)
	=
H		R

sinα		cosβ
	=
H		R

H*cosβ=R*sinα

	R*sinα
H =
	cosβ

r		R*sinα		cosβ		cosβ
	=		*		=
H		2sinβ		R*sinα		2sinβ

cosβ		3
	=
2sinβ		4

	6sinβ		3sinβ
cosβ =		=
	4		2

sin²β+cos²β=1

	9sin2β
sin2β+		= 1 /*4
	4

4sin²β+9sin²β=4 13sin²β=4 sin²β=⁴₁₃

	2		2√13
sinβ =		=
	√13		13

	3√13
cosβ =
	13

	H2
sinβ =
	R

	H
sinβ=
	2R

H = 2R*sinβ

	2√13		4R√13
H = 2R*		=
	13		13

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− cosβ=^r_R r = R*cosβ

	3R√13
r =
	13

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− teraz wystarczy podstawić do wzorów

Miki: Można też prościej:

r		3
	=
h		4

to: r=³₄*h teraz z tw. Pitagorasa w trójkącie prostokątnym: o wymiarach; r, ^h₂ i R (^h₂)² +(³₄h)² = R^{2 h2}₄ +⁹₁₆h² = R^{2 13}₁₆h² = R² h² = ^16R2₁₃

	4R√13
h=
	13

	3R√13
to: r=34*h => r=
	13