geometria analityczna Jula122: Zbadaj, czy prosta o równaniu 4x − y −3 = 0 jest symetralną odcinka o końcach: A=(−3, 2) i B=(5, 0) Poproszę o wyjaśninie.

Aga1.: Trzeba znaleźć równanie symetralnej i porównać z daną, czy są identyczne.

Artur_z_miasta_Neptuna: symetralna dzieli odcinek 'na pół' innymi słowy: krok 1: wyznaczasz prostą przechodzącą przez A i B krok 2: wyznaczasz punkt przecięcia się prostych (punkt C) krok 3: wyznaczasz odległość AC i BC ... i sprawdzasz czy są równe lub krok 1: stosujesz wzór na odległość punktu od prostej i sprawdzasz czy punkty A i B są 'równo odległe' od prostej UWAGA w drugiej metodzie może dojść do fałszywego pozytywnego wyniku, jeżeli prosta została tak paskudnie dobrana, że jest ona np. równoległa do wektora AB

Aga1.: Można np. tak. 1) znaleźć S środek odcinka AB. 2) znaleźć współczynnik kierunkowy prostej AB. 3) napisać równanie prostej prostopadłej do pr. AB (w postaci ogólnej)przechodzącej przez punkt S

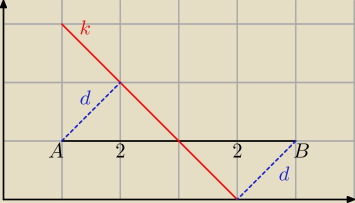
Artur_z_miasta_Neptuna: Aguś ... ale symetralna nie musi być postopadła do wektora AB

Vizer: http://pl.wikipedia.org/wiki/Symetralna_odcinka

Artur_z_miasta_Neptuna: mea culpa (czy jak to się pisze) ... za głupotę którą właśnie palnąłem

Saizou : https://matematykaszkolna.pl/strona/3385.html Arturze kliknij

Artur_z_miasta_Neptuna: no już nie bijcie mnie nie bijcie toć przeprosiłem

Vizer: na zaś

Basia: A(−3;2) B(5;0) P∊sym.AB ⇔ |AP| = |BP| ⇔ AP² = BP² ⇔ (x+3)²+(y−2)² = (x−5)²+(y−0)² ⇔ x²+6x+9+y²−4y+4 = x²−10x+25+y² ⇔ 6x−4y+13 = −10x+25 ⇔ −4y = − 16x+12 ⇔ y = 4x−3 czyli sym.AB ma równanie y = 4x−3 (4x − y − 3 = 0)

Eta: 2 sposób środek odcinka AB S( 1,1)

	−1
wsp. kierunkowy prostej AB : aAB=
	4

	−1
to sym. AB: y=		(x−xS)+yS ⇒ y= 4x−3
	aAB

⇒4x−y−3=0 −−− jest symetralną odcinka AB