Oblicz pole figury ograniczonej wykresami funkcji f(x)= |x+4| - |x| i g(x)= |2x| kacperek: Oblicz pole figury ograniczonej wykresami funkcji f(x)= |x+4| − |x| i g(x)= |2x|

Basia: najpierw trzeba zapisać wzory funkcji bez wartości bezwzględnej 1. x∊(−∞; −4) ⇒ |x+4| = −x−4 i |x|= −x ⇒ f(x) = −x−4−(−x) = −4 x∊<−4;0) ⇒ |x+4| = x+4 i |x| = −x ⇒ f(x) = x+4−(−x) = 2x+4 x∊<0;+∞) ⇒ |x+4| = x+4 i |x| = x ⇒ f(x) = x+4−x = 4 2. x∊(−∞;0) ⇒ |2x| = −2x ⇒ g(x) = −2x x∊<0;+∞) ⇒ |2x| = 2x ⇒ g(x) = 2x narysuj to sobie teraz i napisz czy dalej to ma być rozwiązane metodą szkolną czy przy pomocy całek

kacperek: metoda szkolna

Basia: no to po narysowaniu będziesz tam miał dwa trójkąty: ABC: A(0,0) B(−1;2) C(0;4) i ACD: A(0;0) C(0;4) D(2;4) z tym już powinieneś sobie poradzić

pigor: ... np. tak : f(x)=g(x) ⇔ |x+4|−|x|= 2|x| ⇔ {x+4|= 3|x| /² ⇔ x²+8x+16= 9x² ⇔ x²−x−2=0 ⇔ ⇔ x²−2x+x−2=0 ⇔ x(x−2)+1(x−2)=0 ⇔ (x−2)(x+1)=0 ⇔ x=−1 ∨ x=2 , to szukane pole np. tak : P_f = ¹₂(6+4)*|2−(−1)| − ¹₂*|−1|*4−¹₂*2*6= 5*3−2−6= 15−8= 7 j².

kacperek: dziękuję

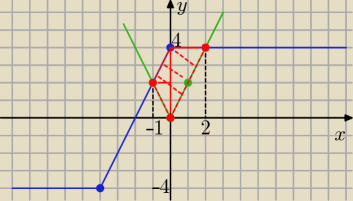
Eta: Odp: P= 6[j²]] ........ pigor] ?