Trójkąty Jolcia: Wyznacz równanie wysokości trójkąta ABC wychodzącej z A, gdy: A(−1,−2) B(−1,−3) C(1,−2)

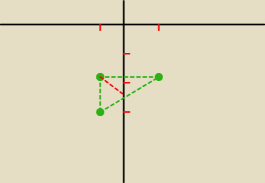
kropka: AB=1 AC=2 BC=x 1²+2²=x² 1+4=x² x=√5 pole trójkąta prostokątnego ax/2 P=2*√5/2 P=√5 Pole trójkąta P=x*h/2 2P=xh h=2P/x h=2 √5/p{5) h=2 może ktoś sprawdzić bo nie jestem pewna..

pazio: ten pierwszy wzór na pole masz źle. powinno być:

	1
P =		|AB||AC| = 1
	2

więc

	1
P =		*h|BC|
	2

2 = √5h

	2√5
h =
	5

@Basia: Nie o to chodziło w tym zadaniu. Należy wyznaczyć równanie wysokości, a nie liczyć jej długość. Trzeba napisać równanie prostej BC, a potem równanie prostej do niej prostopadłej przechodzacej przez punkt A.

@Basia: Piszemy równanie prostej BC B(−1,−3) C(1,−2) y = ax+b −3 = a*(−1)+b −a + b = −3 −−−−−−−−−−−−−−−−−−−−− −2 = a*1+b a+b = −2 −−−−−−−−−−−−−−−−−−−−−−− dodajemy stronami 2b = −5 b = −⁵₂ a−⁵₂ = −2 a = −2+⁵₂ a = ¹₂ pr.BC y = ¹₂x−⁵₂ prosta k, w której zawiera się wysokość AA₁ jest prostopadła do BC

	1
a1 = −1a = −		= −2
	12

y = −2x + b₁ A(−1,−2)∊k −2 = −2*(−1)+b₁ −2 = 2+b₁ b₁ = −4 k: y = −2x − 4