Oblicz długości boków trójkąta
Mati00721: Miara największego kąta w trójkącie jest dwa razy większa od miary jego najmniejszego kąta.
Oblicz długości boków tego trójkąta, jeżeli są one kolejnymi liczbami naturalnymi.
4 wrz 15:21
Basia:
Mati00721 próbowałam to policzyć na różne sposoby
ale twierdzenie sinusów nic nie daje
no tylko tyle, że n>3
może z tw.cosinusów, ale rachunki będą paskudne
jesteś pewny, że dobrze przepisałeś pełną treść zadania ?
5 wrz 05:34
Basia:
P.S. mogłam się też pomylić w rachunkach, jeszcze sprawdzę, ale Ty też sprawdź
5 wrz 06:53
ania: te boki to 4,5,6
5 wrz 07:38
ania: z twierdzenia sinusów tylko
5 wrz 07:39
ania: no i oczywiście trygonometria ;>
5 wrz 08:09
Aga1.:
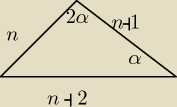
| n | | n+2 | | n+1 | |
| = |
| = |
| |
| sinα | | sin2α | | sin(1800−3α) | |
| n | | n+2 | | n+2 | | 2 | |
| = |
| ⇒n= |
| ⇒n= |
| |
| sinα | | 2sinαcosα | | 2cosα | | 2cosα−1 | |
| n | | n+1 | |
| = |
| |
| sinα | | sinα(3cos2α−sin2α) | |
nsinα(3cos
2α−sin
2α)=(n+1)sinα /:sinα , bo sinα>0
| 2 | | 2 | |
| (3cos2α−(1−cos2α))= |
| +1 /*(2cosα−1) |
| 2cosα−1 | | 2cosα−1 | |
2(4cos
2α−1)=1+2cosα
8cos
2α−2cosα−3=0
Δ=100
| | 3 | | −1 | |
cosα= |
| v cosα= |
| −−−−odpada, bo cosα>0 |
| | 4 | | 2 | |
n+1=5
n+2=6
5 wrz 08:44
Aga1.: Lub prościej
2ncosα=n+2
i teraz z twierdzenia cosinusów
n
2=(n+1)
2+(n+2)
2−2(n+1)(n+2)cosα
Po podstawieniu za cosα i wykonaniu działań
2n
2−6n−8=0/:2
n
2−3n−4=0
n=4 Vn=−1 odpada
n+1=5
n+2=6
5 wrz 09:03
Bogdan:
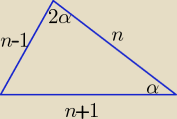
Tak samo, ale jeszcze prościej przez zmianę oznaczeń (bez Δ):
| n−1 | | n+1 | | n+1 | |
| = |
| ⇒ 2sinαcosα * (n−1) = sinα * (n+1) ⇒ cosα = |
| |
| sinα | | sin2α | | 2(n−1) | |
| | n+1 | |
(n−1)2 = n2+(n+1)2−2n(n+1)*cosα ⇒ n2−2n+1=n2+n2+2n+1−2n(n+1)* |
| |
| | 2(n−1) | |
| n(n+1)2 | | n−1 | |
| =n2+4n /* |
| ⇒ n2+2n+1=n2−n+4n−4 ⇒ n=5 |
| n−1 | | n | |
Odp.: n−1=4, n=5, n+1=6
5 wrz 10:20
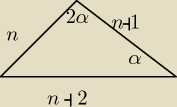
 Tak samo, ale jeszcze prościej przez zmianę oznaczeń (bez Δ):
Tak samo, ale jeszcze prościej przez zmianę oznaczeń (bez Δ):