Znajdź parametr m Mati00721: Dla jakiej wartości parametru m rozwiązaniem równania |x−1|=m+2 jest para liczb o przeciwnych znakach?

Artur_z_miasta_Neptuna: |x−1|=m+2 ⇔ |x−1|−2 = m najłatwiej to zadanie rozwiązać ... graficznie narysuj sobie funkcję f(x) = |x−1| −2 i już widzisz dla jakich 'm' (np. m=1 to linia prosta równoległa do osi OX) będziesz otrzymywał żądane rozwiązania.

Bogdan: Podaj Arturze przykład liczby, która wstawiona w miejsce parametru m spełni warunki zadania.

Artur_z_miasta_Neptuna: hmm m=8 chociażby tak naprawdę to m∊(−1; +∞) −−− rysuję wykres w pamięci więc proszę się nie śmiać z ewentualnego błędu z początkowym przedziałem

Artur_z_miasta_Neptuna: dla m=−1 rozwiązaniami jest x=0 ⋀ x=2 ... więc dla m>−1 będzie już ujemna i dodatnia

Piotr: o ile dobrze kombinuje to nie ma takiej liczby, prawda Bogdan ?

Bogdan: Dla m = 8 |x − 1| = 8 + 2 ⇒ |x − 1| = 10 x − 1 = −10 ⇒ x = −9 lub x − 1 = 10 ⇒ x = 11 Liczby −9 i 11 nie są przeciwne

Artur_z_miasta_Neptuna: Piotr ... a liczby x=−1 i x=3 (dla m=0) nie są przeciwnych znaków

Artur_z_miasta_Neptuna: Bogdan: "o przeciwnych znakach" tutaj nie mają być przeciwne ... mają mieć inne znaki, czyli x₁*x₂ <0

Bogdan: Co to są liczby przeciwne?

Bogdan: Nie śmieję się Arturze. W zadaniu chodzi o parę liczb o przeciwnych znakach, a nie o liczby przeciwne. Chciałem uszczegółowić Twoją wypowiedź.

Artur_z_miasta_Neptuna: Bogdan ... ale co chcesz uszczegółowić W zadaniu należy podać dla jakiego parametru 'm' rozwiązania będą miały przeciwne znaki ... i tyle. rozwiązania nigdy nie będą przeciwne bo |x−1|−2 nie jest funkcją parzystą.

Bogdan: Masz rację Arturze, niefortunnie się wyraziłem i niestarannie odczytałem polecenie w tym zadaniu. Proponuję rozwiązać to zadanie algebraicznie, bez rysunku.

Eta: |x−1|= m+2 ma dwa różne rozwiązania to m> −2 x−1= m+2 v x−1= −m−2 x= m+3 v x= −m −1 Z treści zadania obydwa rozwiązania mają być różnych znaków to iloczyn ( m+3)(−m−1) <0 i m>−2 (m+3)(m+1) >0 i m> −2 odp: m€ (−1,∞)

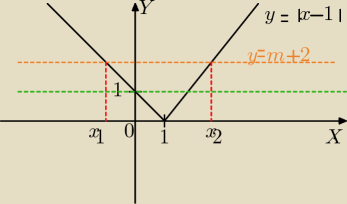
Mila: Metoda graficzna: Dla m+2>1 prosta y=m+2 przetnie wykres w dwóch punktach, których odcięte mają przeciwne znaki. m+2>1⇔m>−1 Metoda algebraiczna: x−1=m+2 lub x−1=−m−2 i m+2≥0 x=m+3 lub x=−m−1 i m≥−2 (m+3)(−m−1)<0 i m≥−2 m>−1