trapezy potrzebujący pomocy: Udowodnij dlaczego dwa trapezy równoramienne nie są podobne.

Artur z miasta Neptuna: Jakie trapezy rownoramienne?

Aga1.: Są trapezy równoramienne, które są podobne.

asdf: bo mają różne kąty

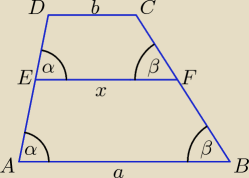
Bogdan: Rację ma Aga1 mówiąc, że istnieją trapezy równoramienne, które są podobne. W dowolnym trapezie ABCD odcinek EF łączący ramiona i równoległy do podstaw AB i CD dzieli trapez ABCD na dwa trapezy podobne.

	a		x
		=		⇒ x = √ab
	x		b

Długość odcinka EF jest równa średniej geometrycznej podstaw AB i CD. Taki odcinek EF istnieje w każdym trapezie, również w trapezie równoramiennym. Można więc zbudować dwa trapezy podobne dzieląc dowolny trapez, a więc i trapez równoramienny na dwa trapezy podobne odcinkiem EF spełniającym warunek: |EF| = √ |AB| * |CD| .

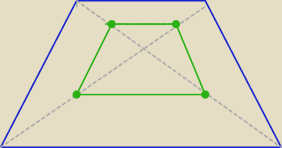
Eta: A takie?

Bogdan:

Artur z miasta Neptuna: ale tutaj nie mamy co się rozczulać nad tym zadaniem. Autor tematu po prostu rzucił wyrwany z kontekstu zdanie i myśli, że wszystko jest jasne. To tak samo jakbym napisał − wykaż, że te liczby nie są parzyste ... albo: te dwie proste nie są równoległe. Drogi autorze − bez danych to mi nic nie zrobimy, bo co prawda jest nieskończenie wiele trapezów równoramiennych, które nie są podobne ... ale dla każdego trapezu równoramiennego istnieje nieskończona liczba trapezów podobnych.

Eta:

potrzebujący pomocy: Przepraszam ale źle napisałem , przez pomyłkę połączyłem część jednego zadania z częścią zadania drugiego. Prawidłowo brzmi to tak: Czy każde dwa trapezy równoramienne są podobne?

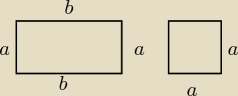
Artur_z_miasta_Neptuna: odpowiedź brzmi ... nie. przykład (patrz rysunek) −−− prostokąt i kwadrat to 'szczególne' przypadki trapezów równoramiennych.