ciagi misia: Ciąg określony wzorem ogólnym an= n(kwadrat)−3n+2 jest a= stały b=rosnący c=malejący d=niemalejący

Basia: policz kilka początkowych wyrazów i pomyśl co należałoby uzasadnić potem dopiero trzeba by było wniosek udowpdnić

Piotr: @misia wez zapisuj to porzadnie. tu masz przyklady: https://matematykaszkolna.pl/forum/przyklady9.html

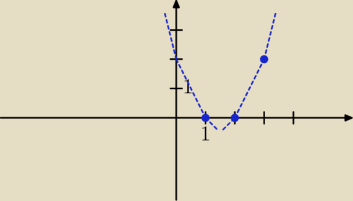
Gustlik: Za pomocą funkcji: a_n=n²−3n+2 y=x²−3x+2 To zwykła parabola.

	b		3
p=−		=
	2a		2

a₁=1−3+2=0 a₂=4−6+2=0 a₃=9−9+2=2 Odp. d − niemalejący

ICSP: n^⬠

asdf: n² − 2n − n + 2 n(n − 1) − 2(n − 1) (n − 1)(n − 2) a > 0 czemu "niemalejący", a nie rosnący?

Gustlik: Bo masz dwa wyrazy równe − a₁=a₂=0, a potem od a₃ rosną. Gdyby ciąg był rosnący, to nie mógłby mieć wyrazów równych.

asdf: a no Oczywista oczywistość

___std__call___: Gustlik − mógłbyś coś więcej napisać o tej metodzie badania ciągów? Gdzieś widziałem już pisałeś na ten temat ale niestety nie mogę tego znaleźć. Pozdrawiam!

___std__call___: Mam na myśli to potraktowanie ciągu jako funkcji i rysowanie wykresu.

Mateusz: Ciąg jest funkcją któej dziedziną jest zbior liczb naturalnych dodatnich i pamietanie tego znacznie usprawnia i ułatwia analize ciągów np przy monotonicznosci majac np ciąg 3n+2 wiemy bez badania roznicy itp ze jest rosnący bo funkcja liniowa ktorej a jest większe od zera jest rosnąca

Gustlik: ___std__call___], tak, jak napisał [P[Mateusz, ciąg jest funkcją, której dziedziną jest zbiór liczb naturalnych dodatnich. Jeżeli ciąg jest dany wzorem łatwej do zbadania funkcji, możemy się posłużyć własnościami tejże funkcji. Czasem można monotoniczność odczytać ze wzoru, np. z wartości określonych współczynników. Np. ciąg arytmetyczny jest funkcją liniową, a jego różnica jest równa współczynnikowi kierunkowemu prostej. Takim ciągiem jest ciąg podany przez Mateusza a_n=3n+2. Jest to ciąg arytmetyczny o róznicy r=a=3, zatem bez liczenia − ze wzoru widać, że ciąg jest rosnący, bo rosąca jest funkcja y=3x+2. Łatwo jest zbadać też ciągi geometryczne − te z kolei w większości przypadków są odpowiednikami funkcji wykładniczych. Wiadomo, ze funkcja y=a^x roście, gdy a>1 i maleje, gdy a∊(0, 1). Czyli np. ciąg a_n=2ⁿ będzie rosnący, tak jak funkcja y=2^x, bo a=2>1, a ciąg a_n=(0,9)ⁿ będzie malejacy, tak jak funkcja y=(0,9)^x, bo 0<0,9<1. Natomiast ciągi geometryczne o ujemnej podstawie potęgi, np. a_n=(−2)ⁿ będą niemonotoniczne, znaki ich wyrazów są naprzemienne +/−/+/−/ itd. W przypadku ciągów "kwadratowych" (czyli takich, jak ten w zadaniu) wykresem są punkty na paraboli − wystarczy obliczyć współrzedną p wierzchołka paraboli i narysować przybliżony wykres funkcji kwadratowej pamiętając, że gdy a>0 − to ramiona paraboli idą w górę, a przy a<0 − idą w dół i z paraboli odczytać, jak zachowuje się ten ciąg dla liczb N₊. Ciąg "kwadratowy" może być niemonotoniczny, gdy p>1. Łatwy do zbadania tą metodą jest ciąg "homograficzny", czyli mający postać funkcji

	2		2
homograficznej. Np. ciąg an=		+1 jest malejacy, bo funkcja y=		+1 jest malejąca w
	n		x

	1		1
zbiorze N+, a ciąg an=−		+4 jest rosnący, bo funkcja y=−		+4 jest rosnąca w
	n		x

zbiorze N₊. Ciąg "homograficzny" może być niemonotoniczny, gdy asymptota pionowa odpowiadającej mu funkcji homograficznej znajdzie się po prawej stronie osi OY, np. takim ciągiem będzie

	2
an=		+4, będzie miał asymptotę pionową x=3,5. Do wyrazu a3 bedzie malał, a potem
	n−3,5

	2
"skoczy" i od a4 będzie znów malał. Wystarczy narysować hiperbolę y=		przesuniętą o
	x

wektor w=[3,5 ; 4] i z hiperboli odczytać własności tego ciągu.

___std__call___: Super! Bardzo dziękuję Gustlik i Mateusz za pomoc! Podobają mi się Gustlik Twoje metody rozwiązywania różnych problemów .