 Witam, mam kilka zadań ze szkoły średniej (p. podstawowy), z którymi sobie nie potrafię
poradzić. Mogę prosić o Waszą pomoc? Oto te zadania:
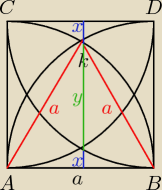
1) Dany jest kwadrat ABCD o boku a. Punkt K jest punktem wspólnym okręgów o(A,a) i o(B,a),
punkt L jest punktem wspólnym okręgów o(C,a) i o(D,a), przy czym oba punkty należą do kwadratu
ABCD. Wyznacz odległość między punktami K i L.
Odp: a(√3−1)
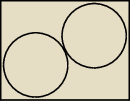
2) W prostokąt o bokach długości 24 i 32 wpisano w sposób pokazany na rysunku (powyżej) dwa
styczne okręgi o równych promieniach. Oblicz długość promieni okręgów.
Odp: 28−8√6
3) Prosta k jest styczna do okręgu o(S,r) w punkcie K, prosta l przecina ten okrąg w punktach L
i M. Punkt A jest punktem wspólnym prostych k oraz l i punkt M należy do odcinka LA.
Uzasadnij, że jeżeli odległość punktu M od punktu K jest równa długości odcinka MA, to
odległość punktu L od punktu K jest równa długości odcinka AK.
Witam, mam kilka zadań ze szkoły średniej (p. podstawowy), z którymi sobie nie potrafię
poradzić. Mogę prosić o Waszą pomoc? Oto te zadania:
1) Dany jest kwadrat ABCD o boku a. Punkt K jest punktem wspólnym okręgów o(A,a) i o(B,a),
punkt L jest punktem wspólnym okręgów o(C,a) i o(D,a), przy czym oba punkty należą do kwadratu
ABCD. Wyznacz odległość między punktami K i L.
Odp: a(√3−1)
2) W prostokąt o bokach długości 24 i 32 wpisano w sposób pokazany na rysunku (powyżej) dwa
styczne okręgi o równych promieniach. Oblicz długość promieni okręgów.
Odp: 28−8√6
3) Prosta k jest styczna do okręgu o(S,r) w punkcie K, prosta l przecina ten okrąg w punktach L
i M. Punkt A jest punktem wspólnym prostych k oraz l i punkt M należy do odcinka LA.
Uzasadnij, że jeżeli odległość punktu M od punktu K jest równa długości odcinka MA, to
odległość punktu L od punktu K jest równa długości odcinka AK.
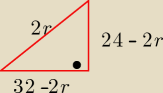
 promień okręgu to r. druga przyprostokątna ma długość 24−2r i jedziesz z Pitagorasa.
promień okręgu to r. druga przyprostokątna ma długość 24−2r i jedziesz z Pitagorasa.

| a√3 | ||
trójkąt równoboczny ABK o boku a wyliczam sobie wysokość ze wzoru h= | ||
| 2 |
| a√3 | ||
h=y+x czyli | =y+x | |
| 2 |
| a−y | ||
x= | ||
| 2 |
| a√3 | ||
podstawiam x do równania | =y+x i dalej już chyba wiesz jak | |
| 2 |

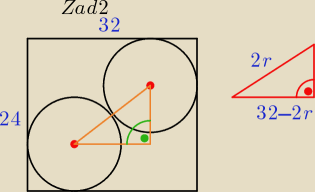
 zad2/ Rysunek, tak jak podał Ci loitz
przy założeniu,że 24−2r >0 i 32−2r >0 ⇒ r€(0,12)
i tw. Pitagorasa ....... wyznacz "r" pamiętając o założeniu
zad2/ Rysunek, tak jak podał Ci loitz
przy założeniu,że 24−2r >0 i 32−2r >0 ⇒ r€(0,12)
i tw. Pitagorasa ....... wyznacz "r" pamiętając o założeniu
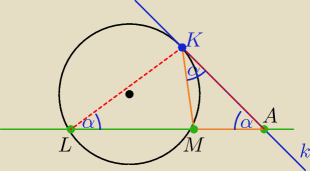 zad.3/
|∡AKM|= |∡MLK| =α −−−jako kąty dopisany i wpisany
ΔMKA jest równoramienny , bo |MK|=|MA| z założenia to |∡MAK|=α
zatem ΔLAK jest też równoramienny o ramionach |LK|= |AK|
co kończy dowód
zad.3/
|∡AKM|= |∡MLK| =α −−−jako kąty dopisany i wpisany
ΔMKA jest równoramienny , bo |MK|=|MA| z założenia to |∡MAK|=α
zatem ΔLAK jest też równoramienny o ramionach |LK|= |AK|
co kończy dowód
| a√3 | ||
ΔABK − Δrównoboczny o boku a, h= | ||
| 2 |
| a√3 | ||
x=a−h=a− | ||
| 2 |
| a√3 | a√3 | |||
|KL|=h−x= | −(a− | )= | ||
| 2 | 2 |
 Witaj Mila
Witaj Mila 
 Miały być nowości od nowego roku szkolnego i....?
Miały być nowości od nowego roku szkolnego i....?

