Rozwiąż trójkąt Maarta: Środkowe poprowadzone w wierzchołków A i B trójkąta prostokątnego równoramiennego ABC o ramieniu długości 6 cm przecinają się w punkcie P. Rozwiąż trójkąt ABP.

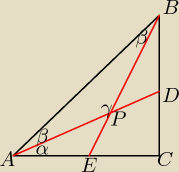
Basia: trójkąty AEB i BDA są przystające

	3		1
tgα=		=
	6		2

sinα		1
	=
cosα		2

cosα = 2sinα sin²α+4sin²α = 1

	1
sin2α =
	5

	√5
sinα =
	5

	2√5
cosα=
	5

sinβ = sin(45−α) = sin45*cosα − sinα*cos45 =

√2		2√5		√5		√2
	*		−		*		=
2		5		5		2

2√10		√10		√10
	−		=
10		10		10

	10		9
cos2β = 1 −		=
	100		10

	3		3√10
cosβ=		=
	√10		10

γ=180−2β

	√10		3√10		2*3*10
sinγ=sin(180−2β) = sin(2β) = 2sinβcosβ = 2*		*		=		=
	10		10		100

	3
	5

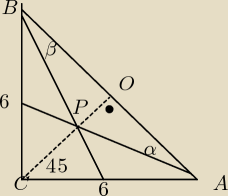AB = 6√2 AP = BP liczysz z tw.sinusów nie wykluczam, że da się w prostszy sposób

Mila: |AB|=6√2 |OC|=3√2

	1
|OP|=		|OC| =√2
	3

w ΔAOP : |PA|²=(3√2)²+√2² |PA|=2√5 |PB|=|PA|

	√2		1
tgα=		=
	3√2		3

|

Mila:

	1
α=β i tgα=
	3

AB=6√2 AP=BP=2√5

Eta: A taki sposób: długości boków ΔAPB ; |AP|=|BP|= 2√5 , |AB|= 6√2

	3√2		3√10
sinβ=		=		⇒ β=..... z tablic i 2β=...
	2√5		10

α= 90^o −β=....

Eta:

	1
Tak Mila tgα=
	3

Chciałam tylko pokazać,że ten sam wynik podała Basia z rozbudowanej trygonometrii