Wyznacz wzór funkcji liniowej f, parametr m i a Mati00721: Zad.1 Miejsca zerowe dwóch funkcji liniowych są liczbami odwrotnymi. Wykresy tych funkcji przecinają się w punkcjie (2,4) i wraz z osią OX ograniczają trójkąt o polu 4. Wyznacz wzory tych funkcji. Zad. 2 Dla jakich wartości parametru m rozwiązaniem układu równań

	⎧	my−9x=−4
	⎩	mx−y=m

jest para liczb (x,y) spełniająca nierówność x+y≥1? Zad. 3 Wyznacz liczbę rozwiązań równania w zależności od parametru a: 1+4x=6a−x.

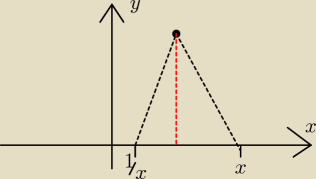
ICSP: bardzo ale to bardzo przykładowy rysunek. P_Δ = 4 P(2;4) ⇒ h = 4

	1		1
PΔ =		a * h gdzie a = x −
	2		x

mam więc równanie :

	1		1
4 =		(x −		) * 4
	2		x

1		1
	(x −		) = 1
2		x

	1
(x −		= 2
	x

x² − 2x − 1 = 0 ⇒ x₁ = 1 − √2 v x₂ = 1 + √2 1^o Rozpatruje x₁ . Aby ustalić wzór prostej wystarczy że będę miał dwa punkty. Jeden : P(2;4) drugi (1 + √2 ; 0)

	0 − 4
a =		= U{4}{1 − √2 = −4 −4√2
	1 + √2 − 2

nasza prosta jest w postaci : f(x) = (−4 − 4√2)x + b 4 = (−8 − 8√2) + b b = 12 + 8√2 f(x) = (−4 − 4√2)x + 12 + 8√2 teraz policzmy równanie drugiej prostej. Wiemy że będą do niej należały punkty: P(2;4), oraz

	1
(		; 0)
	x1

	1
liczymy		= U{1}{1 + √2 = √2 − 1
	x1

	0 − 4		−4		−4(√2 + 3)		4
a2 =		=		=		=		*(√2 + √3)
	√2 − 1 − 2		√2 − 3		2 − 9		7

	4
g(x) =		*(√2 + √3)x + b2
	7

	8
4 =		*(√2 + √3) + b2
	7

	8
b2 = 4 −		*(√2 + √3)
	7

	4		8
g(x) =		*(√2 + √3)x +4 −		*(√2 + √3)
	7		7

2^o Rozważamy x₂ − zostawiam już tobie Czekam teraz na potwierdzenie kogoś lepszego

ICSP: Zad2. Tutaj wystarczy tylko z metody wyznaczników policzyć x oraz y a następnie podstawić to do nierówności i ją rozwiązać. Nic trudnego.

ICSP: Zad3 1 + 4x = 6a − x 5x = 6a − 1

	6a − 1
x =		⇒ Dla każdego a∊R istnieje jedno rozwiązanie.
	5

Mila: x₁, x₂ mam takie same.

Basia: ad.1

	1
a kto powiedział, że		< x ?
	x

trzeba rozważyć dwa przypadki

	1
a = x−
	x

lub

	1
a =		− x
	x

ICSP: mój błąd

Mila: Nie na tym, Basiu polega problem.

Mila: ICSP założył dodatnie x i odwrotność, to wtedy dobrze zapisał, a może być ujemne..... ( Δ rozwartokątny)

Basia: a jaki tu w ogóle jest problem ? bo nie bardzo rozumiem............ 1.

1
	(x−1x)*4 = 4
2

x − ¹_x = 2 x² − 2x − 1 = 0 Δ = 4 + 4 = 8 √Δ = 2√2

	2−2√2		1		1		1+√2
x1 =		= 1−√2 ⇒		=		=		= −1−√2
	2		x1		1−√2		1−2

	1
x2 = 1+√2 ⇒		= −1+√2
	x2

i piszemy równania prostych: pr.AC gdzie A(1−√2;0) C(2;4) pr.BC gdzie B(−1−√2;0) C(2;4) 2.

1
	(1x−x)*4 = 4
2

1
	− x = 2
x

1 − x² = 2x x² + 2x −1 = 0 dalej tak samo (rozwiązania chyba będą te same)

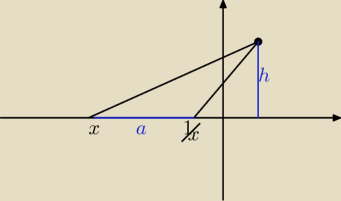
Basia: a jakie to ma znaczenie ?

Basia: tak czy siak

	1
P =		|x−1x|*4
	2

(dlaczego te ułamki takie dziwne ?)

Mila: Chodzi mi o to, że należało zapisać:

	1
Ix−		|=2
	x

Basia:

	1		1		1
|x−		| = 2 ⇔ 1. x−		= 2 ∨ 2.		−x = 2
	x		x		x

pisałam o tym drugim przypadku (chodziło mi o to samo, bo przecież to równoważne)

Mila: To w porządku. Chciałam, aby to zauważył ICSP.

Mila: I oczywiście Mati.

ICSP: Chyba pan ICSP znów zapomniał o tym ze odległość nie może być ujemną

Mila: Na pewno byś znalazł drugie rozwiązanie.