. karolina: dane są dwa wierzchołki kwadratu ABCD : A(−4;0) i C(2;2) wyznacz współrzędne wierzchołków B i D oraz oblicz pole kwadratu proszę o pomoc długość boku to 2√5

loitzl9006: (niewykluczone że jest krótszy sposób) wyznaczasz środek S kwadratu (punkt pomiędzy A i C) potem równanie prostej AC potem równanie prostej BD (prosta prostopadła do AC przechodząca przez punkt S) potem policzyć długość odcinka AS (połowa przekątnej kwadratu) potem zapisać równanie na długość odcinka np. SD wykorzystując fakt, że np. punkt D (x_D, y_D) spełnia równanie prostej BD (czyli D(x_D, f(x_D) gdzie f(x) to równanie prostej BD − dzięki temu będzie tylko jedna niewiadoma x_D) , i że długość odcinka SD jest równa długości odcinka AS. Zauważ, że to równanie będzie miało dwa pierwiastki (bo są tak naprawdę dwa punkty B i D które są równooddalone od środka kwadratu). Te pierwiastki będą współrzędnymi iksowymi punktów B i D. Współrzędne y tych punktów wyliczysz, wstawiając za x współrzędne punktów B i D do równania prostej BD. Tak naprawdę jest nieistotne, który z tych punktów będzie nazwany B, a który D.

karolina: jest jakiś sposób "na współrzędnych"? tzn. czy można to zrobić tak → → AB=CD [Xb−Xa, Yb−Ya] ={Xd−Xc, Yd−Yc] choć w tym wypadku to chyba niewiele mi da bo mam 4 niewiadome. Ale tego typu zadania można tak robić?

loitzl9006: na wektorach tak, jak najbardziej można robić choć teraz wektory są tylko na rozszerzeniu jak chcesz zrobić to wektorami to proponuję skorzystać z równości wektorów → → AB = DC niby masz z tego cztery niewiadome i dwa równania ale y_B możesz uzależnić od x_B i y_D możesz uzależnić od y_D (poprzez równanie prostej BD) i wtedy masz już dwa równania z dwoma niewiadomymi (x_B i x_D)

loitzl9006: * y_D uzależniasz od x_D oczywiście

karolina: ok, dziękuję

Mila: AC − przekątna. Przekątne w kwadracie są równe, prostopadłe i dzielą się na połowy.

	−4+2		0+2
S(		;		)=(−1,1) współrzędne środka AC.
	2		2

wektor SC^→=[3,1] wektor do niego prostopadły i o tej samej długości to; u^→=[1,−3] lub v→[−1,3] S=(−1,1)−−−−−−−−−−T[1,−3]→(0;−2)=B (przesunięcie punktu S o wektor[1,−3]) S=(−1,1)−−−−−−−−−−−T[−1,3]→(−2;4)=D II sposób 1) równanie okręgu ośrodku S i promieniu |SC| 2) równanie prostej AC 3) równanie prostej m prostopadłej do AC, przechodzącej przez S 4) punkty przecięcia okręgu i prostej m. Bardzo pracochłonny sposób

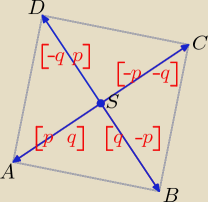
Bogdan: Jest taki sposób. Kiedyś go na forum pokazywałem. Nie chce mi się szukać tego wpisu w archiwum, więc prezentuję go jeszcze raz. Angażujemy wektory. A = (−4, 0), B = (x_B, y_B), C = (2,,2), D = (x_D, y_D), S = (−1, 1), p = −4 −(−1) = −3, q = 0 − 1 = −1, → SA = [p, q] = [−3, −1] → SB = [q, −p] = [−1, 3] → SC = [−p, −q] = [3, 1] → SD = [−q, p] = [1, −3] Teraz zgodnie ze zwrotem wektorów obliczamy współrzędne B i D. x_B = x_S + q = −1 − 1 = −2, y_B = y_S + (−p) = 1 + 3 = 4, B = (−2, 4) x_D = x_S + (−q) = −1 + 1 = 0, y_D = y_S + p = 1 − 3 = −2. D = (0, −2)