pole figury
patka: Jak sie oblicza pole figury ograniczonej tymi liniami?
y=ln(−x), x=−e,y=0
30 sie 14:11
loitzl9006:
z całki pojedynczej
obszar jest ograniczony z góry przez y=ln(−x) a z dołu przez y=0
Granice całkowania: od −e do −1
∫
−e−1 ln(−x) dx = { −x=t −dx = dt dx = −dt x=−e ⇒ t=e x=−1 ⇒ t=1 } =
= − ∫
e1 ln(t)dt
Całkę ∫ ln(t)dt obliczasz przez części
u=ln(t) v'=1
| | 1 | |
∫ ln(t)dt = t * ln(t) − ∫ |
| * t dt = t * ln(t) − ∫ 1 dt = t * ln(t) − t + C |
| | t | |
zatem
− ∫
e1 ln(t)dt = − (t*ln(t) − t) |
1e = (t − t*ln(t) ) |
1e = (1 − 1*ln1 − e + e*lne) =
= 1 − 0 − e + e = 1
30 sie 15:12
Eta:
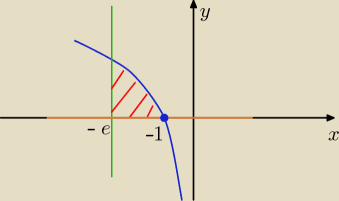
30 sie 15:18
loitzl9006: Obliczając to pole, można nie zmieniać granic całkowania dla t
liczysz całkę nieoznaczoną ∫ ln(−x) dx
wynik podajesz przy pomocy zmiennej x
i potem wstawiasz granice od −e do −1
Eta, łap

za rysunek

30 sie 15:28
Eta:
Dzięki

30 sie 15:36
patka: Wow, dzięki wielkie !
30 sie 16:12

 za rysunek
za rysunek 
