AS:
Ja widzę takie rozwiązanie , chyba poprawne.
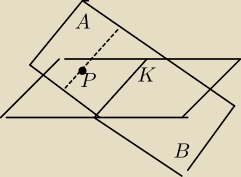
1. Wyznaczyć krawędź wspólną obu płaszczyzn (napisać równanie)
2. Obrać dowolny punkt P w pł. A i poza krawędzią K
3. Napisać równanie prostej przechodzącej przez P i równoległej do krawędzi K.
1. Ustalam równanie krawędzi K
Dla z = 1 mam układ równań
x − y = 0 , 12*x − 15*y = −2
Rozwiązaniem układu: x = 2/3 , y = 2/3
Pierwszy punkt krawędzi: M(2/3,2/3,1)
Dla z = 3 mam układ równań
x − y = −2 , 12*x − 15*y = 6
Rozwiązaniem układu: x = −12 , y = −10
Drugi punkt krawędzi: N(−12,−10,3)
Wektor kierunkowy krawędzi K: w = [2/3 + 12,2/3+10,1 − 3] => w = [38/3,32/3,−2]
Dla uproszczenia rachunków warto przyjąć w1 = 3/2*w = [19,16,−3]
Równanie krawędzi:
x = −12 + 19*t , y = −10 + 16*t,z = 3 − 3*t
2. Obieram dowolny punkt płaszczyzny A np. P(1,2,2)
3. Równanie szukanej prostej równoległej
x = 1 + 19*t , y = 2 + 16*t , z = 2 − 3*t
 Ja widzę takie rozwiązanie , chyba poprawne.
1. Wyznaczyć krawędź wspólną obu płaszczyzn (napisać równanie)
2. Obrać dowolny punkt P w pł. A i poza krawędzią K
3. Napisać równanie prostej przechodzącej przez P i równoległej do krawędzi K.
1. Ustalam równanie krawędzi K
Dla z = 1 mam układ równań
x − y = 0 , 12*x − 15*y = −2
Rozwiązaniem układu: x = 2/3 , y = 2/3
Pierwszy punkt krawędzi: M(2/3,2/3,1)
Dla z = 3 mam układ równań
x − y = −2 , 12*x − 15*y = 6
Rozwiązaniem układu: x = −12 , y = −10
Drugi punkt krawędzi: N(−12,−10,3)
Wektor kierunkowy krawędzi K: w = [2/3 + 12,2/3+10,1 − 3] => w = [38/3,32/3,−2]
Dla uproszczenia rachunków warto przyjąć w1 = 3/2*w = [19,16,−3]
Równanie krawędzi:
x = −12 + 19*t , y = −10 + 16*t,z = 3 − 3*t
2. Obieram dowolny punkt płaszczyzny A np. P(1,2,2)
3. Równanie szukanej prostej równoległej
x = 1 + 19*t , y = 2 + 16*t , z = 2 − 3*t
Ja widzę takie rozwiązanie , chyba poprawne.
1. Wyznaczyć krawędź wspólną obu płaszczyzn (napisać równanie)
2. Obrać dowolny punkt P w pł. A i poza krawędzią K
3. Napisać równanie prostej przechodzącej przez P i równoległej do krawędzi K.
1. Ustalam równanie krawędzi K
Dla z = 1 mam układ równań
x − y = 0 , 12*x − 15*y = −2
Rozwiązaniem układu: x = 2/3 , y = 2/3
Pierwszy punkt krawędzi: M(2/3,2/3,1)
Dla z = 3 mam układ równań
x − y = −2 , 12*x − 15*y = 6
Rozwiązaniem układu: x = −12 , y = −10
Drugi punkt krawędzi: N(−12,−10,3)
Wektor kierunkowy krawędzi K: w = [2/3 + 12,2/3+10,1 − 3] => w = [38/3,32/3,−2]
Dla uproszczenia rachunków warto przyjąć w1 = 3/2*w = [19,16,−3]
Równanie krawędzi:
x = −12 + 19*t , y = −10 + 16*t,z = 3 − 3*t
2. Obieram dowolny punkt płaszczyzny A np. P(1,2,2)
3. Równanie szukanej prostej równoległej
x = 1 + 19*t , y = 2 + 16*t , z = 2 − 3*t
