wielomianom mówimy NIE Saizou : Jakieś zadanko może? <tylko nie zasypujcie mnie nawałem zadań >

Krzychu: Przyłączam się

Eta:

Saizou : Eta to czekamy

Eta: Na co?

Saizou : na zadanko bez wielomianów

Eta: Dowodzik? może być?

Saizou : wrzucaj

Ajtek: Łapcie . W rozwinięciu dwumianu (1+x)ⁿ współczynnik przy x⁴ jest równy współczynnikowi przy x⁸. Oblicz n.

Ajtek: Bry wieczór wszystkim .

Eta:

	1		1		1
zad1/ Wykaż,że dla liczb x,y,z>0 zachodzi : (x+y+z)(		+		+		) ≥ 9
	x		y		z

Saizou : Witaj Ajtek, a widziałeś "wielomianom mówimy NIE"

Eta: zad2/ Dla jakich liczb naturalnych "n" liczba n²+12n+7 jest kwadratem liczby naturalnej ?

Ajtek: Dzie to wielomian

Krzychu: Zresztą Ajtek, to nie poziom maturalny. Może dawniej...

Ajtek: No właśnie dawniej . W moim zbiorku to jest dwumian Newtona

rumpek: za proste dla nich trzeba coś wymyślić

Maslanek: 2) Eta, dla żadnej?

Maslanek:

	n 5		n 8		n n−8
Ajtek,		=		=

Stąd też n−8=5 ⇒ n=13.

Maslanek:

	n 9		n n−9
Brr...		=

n−9=5 ⇒ n=14. Przepisałem bezmyślnie z mózgu xd

Eta: Zad.3/ Wewnątrz trójkąta ABC obrano punkt M. Wykaż,że |∡CMB| > |∡CAB|

Ajtek: No to myśl dalej Maślanek.

Maslanek: No przecież to działa Ajtuś

14 5		14 9
	=		.

Wszystko gra

Ajtek: Zerknij jeszcze raz na treść zadania . Swoją drogą to co napisałeś jest zgodne z prawdą .

Saizou : a miałem dobre chęci żebyście mnie nie zasypywali taką ilością zadań

Maslanek: Przecież n masz podane . n=14. Co jeszcze chcesz?

Maslanek: 15 wyrazów, k=7 znajduje się w środku w jednakowej odległości od 5 i 9. Pasuje

Ajtek: Teoja odpowiedź jest nie do tego zadania

Maslanek: Nie rozumiem chyba Dlaczemu? xd

Ajtek: Co to jest 5 i 9?

Krzychu: Eta mam coś . (y √z−x √z)²+(y √x−z √x)²+(z √y−x √y)²≥0 Jest ok ?

Maslanek: Kolejne wyrazy rozwinięcia dwumianu Newtona

Ajtek: A pytają o 5 i 9?

Krzychu: (y√z−x√z)²+(y√x−z√x)²+(z√y−x√y)²≥0 dla ułatwienia, bo tam spacje

Ajtek: Czy inaczej, piszą coś o 5−tym i 9−tym?

Maslanek: Mam ładniejsze Krzysiek x(y−z)²+y(x−z)²+z(x−y)²≥0

rumpek: Zad. 1/ Okrąg opisany jest na trójkącie ostrokątnym ABC. Styczne do okręgu w punktach A i B przecinają się w punkcie G. Punkt H leży na boku BC i odcinek GH jest równoległy do boku AC. Wykazać, że |AH|= |HC|.

Maslanek:

	n 4		n 8
No cosik tak. 5−ty wyraz (czyli		x4) jest równy x4*		x4.

Mój błąd xD n=12

Krzychu: faktycznie Maslanek, ale jak tak teraz patrze, to z mojego wyciągne odpowiednio z , x , y to wyjdzie na to samo .

rumpek: Odnośnie: Zad. 1 Ety to wymnożyć wystarczy:

	1		1		1
(x + y + z)(		+		+		) ≥ 9
	x		y		z

x

x

y

y

z

z

1 +

+

+

+ 1 +

+

+

+ 1 ≥ 9

y

z

x

z

x

y

Zauważmy teraz, że można wykorzystać: x² + y² ≥ 2xy ∧ y² + z² ≥ 2yz ∧ x² + z² ≥ 2xz

Maslanek: Obrzydliwe rumpek Twoje mianowniki wzbudzają we mnie odrazę

Saizou : i rumpek popsuł całą zabawę

rumpek: Odnośnie: Zad. 2 Kiedyś też miałem je od Ety i jeżeli się Eta "pomyliła" to brzmi ono: n²+12n+17 To teraz spadam na "Jak rozpętałem II wojnę ... "

b.: @Maslanek: n=12 n=12 jest rozwiązaniem, ale czy nie ma czasem innych rozwiązań?

Maslanek: Wtedy na pewno n=9. n=√k²+19−6 − czyli n≥6. Sprawdzanie dla n≥11 jest bez sensu, bo są odległości między kwadratami większe niż 19. Różnica między kwadratami liczb n²−(n−1)²=2n−1. Kiedy 2n−1=19? ⇔ n=10. Czyli tylko liczba n=9 spełnia kryteria.

Maslanek: Nie ma , x⁸ ogranicza rozwiązania

Timmy: @rumpek n ∊ {−16, 4} ?

Maslanek: Coś się popierzyło k²=81... k=9. A wcześniej zapis (n+6)²−19=k² Czyli (n+6)²=100 Stąd n=4... Tragedia xD

rumpek: n² + 12n + 17 = k² ⇒ (n + 6)² − 19 = k² ⇒ (n + 6)² − k² = 19 ⇒ (n + 6 + k)(n + 6 − k) = 19

⎧	n + 6 + k = 19
⎩	n + 6 − k = 1

⎧	n = 4
⎩	k = 9

Maslanek: Ciekawie Nie pomyślałem o czymś takim prostym i pięknym

Krzychu: O którym zadaniu kto mówi. W drugim wyszło mi 4, więc ok?

Krzychu: rumpek: A czy o k trzeba wspomnieć, ze =9? czy mozna tego nie liczyc?

b.: > Maslanek: Nie ma , x⁸ ogranicza rozwiązania ale dobrze byłoby to chociaż krótko uzasadnić...

Saizou : http://img209.imageshack.us/img209/7774/marlinmonroe.jpg

rumpek: lepiej marlin niż siwiec gratki talentu

rumpek: zamiast zadania robić to rysuje

Eta: Echh ...ten rumpek

Saizou : co mam liczyć jak mi jedno zadanie rozwiązałeś a inne reszta forumowiczów. więc ja siedzę sobie cicho jak myszka bardzo dziękuję

Maslanek: Rozwiązanie algebraiczne wyjaśnia wszystko

Eta: Stary Lubosz

Maslanek: Geometrii nie trawię Będzie trzeba kiedyś przysiąść, a teraz pora się pozabijać

rumpek: czyżby Eta zainteresowała się prawym dolnym rogiem "marlin" ?

Eta: i strawisz

Saizou : moc facebook'a jest olbrzymia

Eta: Dokładnie rumpek

rumpek: trzeba jednak zachować pewną anonimowość

Eta: Zad.4/ tylko dla Saizou ! Wykaż,że liczba : 2010*2011*2012*2013 +1 jest kwadratem liczby naturalnej .

Saizou : anonimowość jest przereklamowana

Eta: Przynajmniej teraz wiem jak wygląda Saizou

Saizou : a czy wygląd liczy się w życiu?

Krzychu: rumpek jest jakaś podpowiedź do Twojego zadania?

rumpek: ale nie wiemy jak wygląda Eta i tego się nie dowiemy

Saizou : zad 4 √2010*2011*2012*2013 +1=4 046 131

rumpek: Krzychu zrób rysunek i wiadome

Eta:

Saizou : zobaczycie rozwinę swój dar do jasnowidzenia i narysuję Jo.., Etę

Eta: Masz to wykazać, a nie policzyć!

Krzychu:

	HG		HA
rumpek:		=		?
	HB		HB

Eta: zad3/ .......... czekam na rozwiązanie

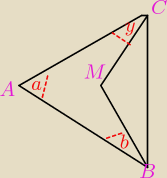
Krzychu: Eta: suma kątów w ABMC jest 180. Kąt BMC rozwarty w tym czworokącie: 180−(α+β+γ) kąt BMC=180−180+(α+β+γ) BMC=α+β+γ

Krzychu: z tą sumą kątów w tym czworokącie, to tak przypuszczam

Krzychu: a nie, jednak nie

Krzychu: suma kątów w ABMC jest 360. Kąt BMC ale po drugiej stronie: 360−(α+β+γ) kąt BMC=360−[360−(α+β+γ)] BMC=α+β+γ

Ania: pomógłby mi ktos z tym zadaniem Czas oczekiwania na autobus linii A jest zmienną losową o rozkładzie wykładniczym z wartością oczekiwaną 10 minut, pani Gosia codziennie dojeżdża do pracy autobusem linii A. Obliczyć prawdopodobieństwo , że traci ona kwartalnie czekając na autobus więcej niż 910 minut, wiedząc że z pracy również wraca autobusem linii A.(zakładamy ze kwartal ma 90 dni)

Krzychu: A ja dobrze zrobiłem Eta Twoje zadanie ?

Eta: ok