pytanie Krzychu: Dla jakich wartości parametru k dane równanie |3^x−1|=k ma jedno rozwiązanie? 3^x−1=k dla x≥0 1−3^x=k dla x<0 x=log₃(k+1)≥0 dla x≥0 i k>−1 x=log₃(1−k)<0 dla x<0 i k<1 Rozwiązując te nierównosći: log₃(k+1)≥log₃1 log₃(1−k)<log₃1 dostaje odpowiednio: k+1≥1 ⇒k≥0 1−k<1 ⇒k>0 Czyli odpowiednio dla x≥0 warunki są k>−1, k≥0 . Mam zrobić ich sumę, część wspólną? oraz dla x<0 warunki k<1, k>0 mam rozpatrzyć sumę, część wspólną? I co dalej?

pigor: ... sprawa jest prostsza niż to twoje pisanie , mianowicie robisz sobie wykres lewej strony równania i widzisz, że k=0 − szukana wartość k, bo spełnia warunek zadania, taki |3^x−1|=0 ⇔ 3^x−1=0 ⇔ 3^x=1 ⇔ x=0 − jedno rozwiązanie . ...

Krzychu: pigor w ogóle nie czaje tego co napisałeś . Ale widzę na rysunku, że jedno rozwiązanie jest dla 0 i od (1,+∞0) ale gdyby było algebraicznie ? Nie wiem czy suma tam czy co ma być.

rumpek: Po co algebraicznie? Takie zadania rozwiązuje się graficznie

Krzychu: Ale ja chce algebraicznie, wiecie co tam powinno być ?

konrad: to ja się wtrącę, pewnie po prostu tego nie umiem robić, ale ja osobiście nie rozumiem jak można odczytywać rozwiązania z wykresu przecież z wykresu nie da się odczytać dokładnego rozwiązania (pomijając, że nie umiem rysować wykresów poza prostymi funkcjami ) dlatego ja też zawsze szukam rozwiązania algebraicznego

Krzychu: Konrad, a tu wiesz co zrobić z tymi warunkami ?

konrad: szczerze to nie wnikałem w Twoje rozwiązanie, bo mi się nie chciało

konrad: zresztą to co pigor tam dalej napisał, te obliczenia, to to jest chyba właśnie rozwiązanie algebraiczne tego

Piotr: chyba nie konrad. dla k=5, k=7 itd. to rownanie tez ma przeciez jedno rozwiazanie.

konrad: aha, czyli pigor się pomylił

konrad: anyway, też chciałbym poznać prawidłowe rozwiązanie algebraiczne tego równana

Maslanek: Algebraicznie: |3^x−1|=k; Zatem k≥0. 3^x−1=k lub 3^x−1=−k (1) x=log₃(k+1) lub (2) x=log₃(1−k). Funkcja logarytmiczna jest różnowartościowa, więc jedno rozwiązanie będzie na pewno, gdy (1)=(2) Zatem k+1=1−k ⇔ k=0. Funkcja (2) jest określona dla k∊(−∞,1), czyli w naszym przypadku k∊<0,1). Funkcja (3) jest określona dla k∊(−1,∞), czyli u nas k∊<0,∞). Stąd też zauważamy, że będziemy mieć dwa rozwiązania w przedziale dla k∊(0,1) − wykluczyliśmy wcześniej k=0 (jednoczesne rozwiązanie równań). Zatem jedno rozwiązanie będzie również dla k∊<1,∞). Ostatecznie jedno rozwiązanie dla k∊{0}∪<1,∞).

Eta: |x−a| =0 ma tylko jedno rozwiązanie zatem: |3^x−1|= k ma jedno rozwiązanie ⇔ k=0 −−− to jest odp: do tego zadania załatwione w jednej linijce ! Gdyby było jeszcze polecenie " wyznacz to rozwiązanie" to: |3^x−1|=0 ⇔ 3^x−1=0 ⇔ 3^x= 1= 3⁰ ⇒ x=0 To samo wyjaśnił Ci pigor ( więc w czym problem?

Maslanek: Eta, czasem |3^x−1| dla x<0 nie przekroczy nigdy wartości k=1? lim (x→−∞) |0−1| = 1 lim (x→0⁻) |1⁻−1|=|0⁻|=0⁺

Maslanek: Nawet na pewno Weź równanie |3^x−1|=2 Wtedy 3^x−1=2 lub 3^x−1=−2 Co daje: 3^x=3 lub 3^x=−1 (sprzeczne)

Krzychu: aha, ale to niepełne rozwiązanie, bo nie obejmuje jeszcze k∊<1,+∞), gdzie też jest jedno rozwiązanie. juz jakoś to zrobiłem, wystarczyło tylko wyłaczyć komputer i sie skoncentrować

Piotr: Eto a ile bedzie rozwiazan np dla k=2?

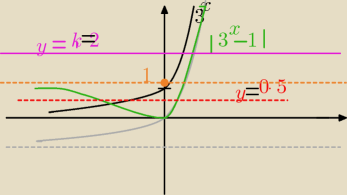
Mila: Przykład dla k=0,5 mamy y=0,5 są dwa rozwiązania dla k=2 jedno rozwiązanie odp Jedno rozwiązanie dla k=0 lub k>1 (przepraszam za "brzydkie" odbicie)

Eta: Echh Słusznie! ... nie wiem czemu pomyślałam funkcji liniowej odp: k€<1,∞) U {0}

Mila: Tak, bywa, ja mam z kolei literówkę: ma być k≥1( co widać na rysunku)

Piotr: Uff Dziękuję za odpowiedzi

pigor: ... no tak ,mało pokory wykazałem przy tym rozwiązaniu, przepraszam, sknociłem po prostu moje ulubione zadanie, z modułem i parametrem , a przez to, bo... "zapomniałem" , że f. wykładnicza y=a^x ma asymptotę poziomą y=0 , a tu po przesunięciu i odbiciu asymptotą staje się prosta y=1 i tyle . ...

baca: Takie proste zadanko i tyle gadania?

Eta: "pogadać" zawsze można