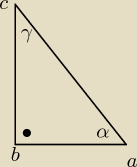
? ?: dł. AB = 6 dł. AC = 2P{10} oblicz tgα * √1−cos²γ +sinα z góry dziękuję

loitzl9006: |BC|=√|AC|²−|AB|² |BC|=√40−36=2

	|BC|		2
sinα=		=		= U{1}{√10
	|AC|		2√10

	|BC|		2		1
tgα =		=		=
	|AB|		6		3

	1
cosγ = cos(90o−α)=sinα=
	√10

	1		1
cos2γ=sin2α=(		)2=
	√10		10

	1		1
tgα * √1−cos2γ + sinα =		* √1−110 +		= ... dokończ
	3		√10

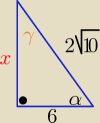Eta: x>0 z tw. Pitagorasa x²= (2√10)²−6² ⇒ x²= 4 ⇒ x=2

	sinα
teraz : cosγ= sinα to 1−sin2α= cos2α i tgα=
	cosα

	sinα
i mamy: tgα*√1−cos2γ+sinα=		*cosα+sinα= sinα+sinα= 2sinα
	cosα

	2		√10
sinα=		=
	2√10		10

	√10
to 2sinα=
	5

2 sposób , możesz podać z trójkąta: tgα =... sinα =... cosγ=.. podstawić dane i to wszystko

?: ok, Dziękuję

	√10
ładnie wychodzi
	2

Eta: Wynik ma być taki:

√10
5