wart bezw klik: zbadaj istnienie i liczbę rozwiązań równania w zależności od parametru m I5−xI−Ix−2I=m

loitzl9006: Podpowiedź: narysuj wykres funkcji f(x)=I5−xI−Ix−2I. Żeby to zrobić, trzeba rozważyć trzy przedziały − umiesz to?

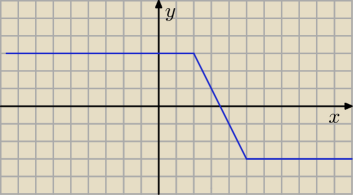
Saizou : f(x)=l5−xl−lx−2l −dla x∊(−∞:2) y=5−x−(−x+2)=5−x+x−2=3 −dla x∊<2:5) y=5−x−(x−2)=5−x−x+2=−2x+7 −dla x∊<5:+∞) y=−5+x−(x−2)=−5+x−x+2=−3 i wystarczy odczytać że − zero rozwiązań dla m ∊(−∞:−3) U (3:+∞) − jedno rozwiązanie dla m∊(−3:3) − nieskończenie wiele dla m∊{3}

loitzl9006: Teraz II sposób na to zadanie (tylko nie wiem czy mnie zrozumiecie ): I5−xI−Ix−2I=m |5−x|=|x−2|+m i teraz rysujemy w jednym układzie współrzędnych wykresy funkcji: |5−x| i |x−2|, przy czym wykres |5−x| "stoi w miejscu", a wykres |x−2| jest "sterowalny góra−dół" przez parametr m. I teraz dla m=0 będzie po prostu |x−2|, zaś np. dla m=1 wykres |x−2| będzie przesunięty o 1 jednostkę w górę, zaś dla m=−2 wykres |x−2| będzie przesunięty o 2 jednostki w dół. Ilość rozwiązań równania to po prostu ilość punktów wspólnych obu wykresów.

klik: rozwiazywałam algebraicznie i powstał mi problem z przedziałem <2,5) wychodzi m≤3 i wtedy dla −3 wychodzi jedno rozwiązanie i jednocześnie nieskończenie wiele rozwiązań dla m=3 każda liczba z przedziału (−∞,2) dla m∊(−3,3> jedno rozwiąznie dla m=−3 każda liczba z przedziału <5,+∞)

klik: nie dl a −3 tylko dla 3 pomyłka

loitzl9006: No to weźmy przedział <2;5> i opuśćmy wartości bezwzględne: wtedy I5−xI = 5−x (bo w przedziale <2;5> wyrażenie 5−x przyjmuje wartość nieujemną Ix−2I = x−2 (bo w przedziale <2;5> wyrażenie x−2 przyjmuje wartość nieujemną liczymy I5−xI−Ix−2I = (5−x)−(x−2)=5−x−x+2=−2x+7 przypuszczam zatem, że robiłaś jakiś błąd przy opuszczaniu wartości bezwzględnych. Rozumiesz to co rozpisałem?

klik: I5−xI zamieniłam na Ix−5I i rozpatrzyłam 1.(−∞,2), 2.<2,5), 3.<5,+∞) w 1. otrzymałam m=3 w 2.m∊(−3,3> w 3.m=−3

loitzl9006: Wniosek: dla m mniejszych od −3, a także większych od 3, równanie nie ma rozwiązań. Ponieważ w 2. przedziale równanie przyjmuje postać −2x+7=m , to widać że takie równania mają jedno rozwiązanie. A skoro w 1. przedziale (po opuszczeniu wart. bezwzględnych) wyszło że I5−xI−Ix−2I=3 to wniosek że dla m=3 równanie ma nieskończenie wiele rozwiązań. Tak samo w 3. przedziale wyszło że I5−xI−Ix−2I=−3 czyli dla m=−3 jest nieskończenie wiele rozwiązań. Przekonasz się o tym, wstawiając do równania dowolne x−sy z przedziału 3. czyli <5,+∞) do wyrażenia I5−xI−Ix−2I. Zawsze wyjdzie wynik −3.

klik: Wszystko się zgadza ale w takim razie idąc algebraicznym rozwiązaniem zgodnie z def. wart. bez. należy w pewnym momencie rozwiązać nierówność podwójną dla przedziału <2,5) 2≤^7−m₂<5 co w konsekwencji daje m∊(−3,3> co wskazuje dla m=3 jedno rozwiązanie

loitzl9006: w przedziale <2;5) zgoda, dla m=3 jedno rozwiązanie (to rozwiązanie to x=2), ale jeszcze w przedziale (−∞;2) dla m=3 jest nieskończenie wiele rozwiązań zatem dla m=3 jedno + nieskończenie wiele = nieskończenie wiele rozwiązań Przekonująco?

klik: tak dzięki bo rozwiązywałam inne tego typu i za każdym razem pojawiał sie ten sam problem na końcu przedziału.