Obwód trapezu równoramiennego opisanego na okręgu równa się 68 cm . Jaką długość wojtek: Obwód trapezu równoramiennego opisanego na okręgu równa się 68 cm . Jaką długość ma ramię tego trapezu ?

Eta: 17 cm

Bogdan: Co wiesz o czworokącie opisanym na okręgu?

Bogdan: Witaj Eto

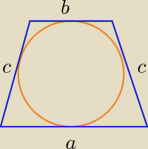
Eta: z warunku wpisania okręgu w trapez a+b= c+c to 4c=68 ⇒ c=.....

Eta: Witam Bogdanie Przepraszam,że popsułam Ci " zabawę "

wojtek: o dzięki nie wiedziałem o tym wzorku

Bogdan: To jeszcze raz wojtku pytam: co wiesz o czworokącie opisanym na okręgu? Nic nie szkodzi Eto

wojtek: wcześniej nic ,a teraz znam ten wzorek

Bogdan: Podaj twierdzenie o czworokącie opisanym na okręgu (poszukaj gdzieś to twierdzenie), a przy okazji inne twierdzenie o czworokącie wpisanym w okrąg.

wojtek: Czworokąt opisany na okręgu Jeżeli na okręgu obierzemy cztery punkty i poprowadzimy przez nie styczne, to punkty przecięcia kolejnych stycznych będą wierzchołkami czworokąta opisanego na okręgu. W czworokącie opisanym na okręgu sumy długości przeciwległych boków tego czworokąta są równe. a + c = b + d Pole czworokąta opisanego na okręgu o promieniu r: P=12r (a+b+c+d) W dowolny czworokąt można opisać na okręgu tylko wtedy, gdy dwusieczne wszystkich jego kątów przecinają się jednym punkcie, który jest środkiem okręgu. Czworokąt wypukły można opisać na okręgu wtedy i tylko wtedy, gdy sumy długości przeciwległych boków czworokąta są równe

Bogdan: O właśnie, chodzi o twierdzenie: "w czworokącie opisanym na okręgu sumy długości przeciwległych boków tego czworokąta są równe". Ta własność potrzebna była w tym zadaniu. Myślę, że znałeś ją.