 Potrzebuję pomocy w zadaniu:
Udowodnij, że w dowolnym trójkącie równobocznym ABC suma odległości dowolnego punktu należącego
do tego trójkąta od baków tego trójkąta jest równa wysokości tego trójkąta...
Potrzebuję pomocy w zadaniu:
Udowodnij, że w dowolnym trójkącie równobocznym ABC suma odległości dowolnego punktu należącego
do tego trójkąta od baków tego trójkąta jest równa wysokości tego trójkąta...

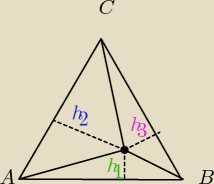
| a2√3 | ||
|AB| = a ⇒ P = | ||
| 4 |
| 1 | 1 | 1 | 1 | |||||
P = | ah1 + | ah2 + | ah3 = | a(h1 + h2 + h3} | ||||
| 2 | 2 | 2 | 2 |
| 1 | a2√3 | ||
a(h1 + h2 + h3} = | |||
| 2 | 4 |
| a√3 | ||
h1 + h2 + h3 = | = h | |
| 2 |
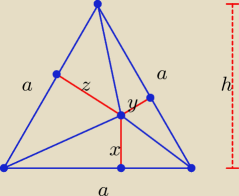 Oblicz pola trójkątów o wysokościach x, y, z i zsumuj je, wynik porównaj z polem
trójkąta równobocznego o boku a i wysokości h
Oblicz pola trójkątów o wysokościach x, y, z i zsumuj je, wynik porównaj z polem
trójkąta równobocznego o boku a i wysokości h
 wybierz dowolny punkt w trojkacie; polacz go z kazdym bokiem (pamietaj, odl. pod katem
prostym); teraz polacz go z kazdym wierzcholkiem; sproboj zapisac sume pol tak utworzonych
trojkatow i przyrownaj ja do pola calego trojkata; cos powinienes zobaczyc
wybierz dowolny punkt w trojkacie; polacz go z kazdym bokiem (pamietaj, odl. pod katem
prostym); teraz polacz go z kazdym wierzcholkiem; sproboj zapisac sume pol tak utworzonych
trojkatow i przyrownaj ja do pola calego trojkata; cos powinienes zobaczyc
| 1 | 1 | 1 | 1 | 2 | ||||||
czyli | ax + | ay + | az = | ah /* | ||||||
| 2 | 2 | 2 | 2 | a |