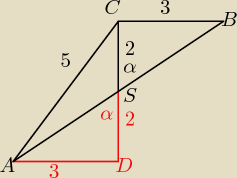
 Po przecięciu zadanego trójkąta ABC wzdłuż środkowej CS można ułożyć trójkąt ADC.
Trójkąty CBS i ADS są podobne (dwa równe boki BS=AS; CS=DS i kąty α), a więc pola trójkątówABC
i ADC są równe, ΔADC jest posiada kąt prosty ADS (trójkąt Pitagorasa 52=32+42).
Przeciwprostokątna AS ΔADS jest równa 1/2 boku AB ΔABC. To powinno wystarczyć resztę oblicz
sam.
Dla sprawdzenia R=5*√13/4
Po przecięciu zadanego trójkąta ABC wzdłuż środkowej CS można ułożyć trójkąt ADC.
Trójkąty CBS i ADS są podobne (dwa równe boki BS=AS; CS=DS i kąty α), a więc pola trójkątówABC
i ADC są równe, ΔADC jest posiada kąt prosty ADS (trójkąt Pitagorasa 52=32+42).
Przeciwprostokątna AS ΔADS jest równa 1/2 boku AB ΔABC. To powinno wystarczyć resztę oblicz
sam.
Dla sprawdzenia R=5*√13/4
| 1 | ||
d= | √2a2+2b2−c2 ,gdzie c to bok na który opuszczono środkową
| |
| 2 |
| 1 | ||
2= | √2*33+2*52−c2
| |
| 2 |
| 8+2√13 | ||
p= | =4+√13
| |
| 2 |
| abc | 5*3*2√13 | 30√13 | 5√13 | |||||
R= | = | = | = | |||||
| 4P | 4*6 | 24 | 4 |

| 3 | 2 | |||
c= 2√13 cosA= | to sinA= | |||
| √13 | √13 |
| 3*2√13 | ||
P= | *sinA= ........ =6 | |
| 2 |
| 5 | 5√13 | |||
2R= | to R= | |||
| sinA | 4 |
