tg x = -2 x ∊ (π/2, π) . wyznacz pozostałe wartości funkcje trygonometryczne ar wojtek: tg x = −2 x ∊ (π/2, π) . wyznacz pozostałe wartości funkcje trygonometryczne argumentu x

krystek: wzór nedynkowy

	sinx
sin2x+cos2x=1 i tgx=
	cosx

a: wykorzystaj to:

	sin x
tg x =
	cos x

cos ² x +sin ² x=1

wojtek: a możecie mi to ładnie rozwiązać ?

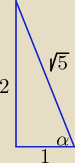Bogdan: Proponuję tak:

	π
Jeśli α∊(		, π), to sinα > 0, cosα < 0, tgα < 0, ctgα < 0
	2

	2		1		1
sinα =		, cosα = −		, tgα = −2, ctgα = −
	√5		√5		2

Zamiast x wziąłem α

krystek: sinx=−2cosx i podstawiasz do "jedynki trygonometr" (−2cosx)²+cos²x=1 dalej próbuj sam .

Eta:

	π
x€ (		,π) −−− II ćw. układu współrzędnych
	2

to ctgx<0 , sinx>0 , cosx<0

	1		1
ctgx=		= −
	tgx		2

sinx
	= −2 ⇒ sinx= −2cosx
cosx

sin²x+cos²x=1

	1		√5		√5
4cos2x+cos2x=1 ⇒ cos2x=		to cosx=		v cosx= −
	5		5		5

	√5
przyjmujemy cosx= −		€ IIćw.
	5

	√5		2√5
sinx= −2*(−		)=		€ IIćw
	5		5

Eta:

	√5
Poprawiam ostatnie zapisy cosx= −		<0
	5

	2√5
sinx=		>0
	5