trapez wpisany w okrag ..: Prosze o podpowiedz. W trapez rownoramienny wpisano okrag. Odleglosc od srodka okregu do punktu przeciecia przekatnych trapezu ma sie do promienia, jak 5 do 13. Wynacz stosunek obwodu trapezu do dlugosci wpisanego okregu.

@Basia: To jest to zadanie. Ja już chyba jestem za bardzo śpiąca żeby je rozgryzać.

Klara: OK . zaraz pomyślę Miłych snów! Dobranoc !

@Basia:

@Basia: Chyba to rozwiązałam. Wyszło mi: a = ³₂r b = ²₃r c = ¹³₁₂r

	13
s =
	4π

z podobieństwa i przystawania trójkątów.

@Basia: Nie, błąd rachunkowy.

@Basia: Teraz chyba dobrze. a=3r b=⁴₃r c=¹³₆r s = ¹³_π

Klara: Wiedziałam ,że nie odpuścisz Zatem idziemy spać Do jutra,

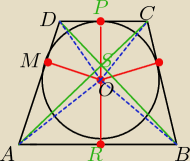
@Basia: OP − promień r dzielę go na 13 odcinków x = ^r₁₃ OS = 5x PS = 8x ^OS_OP = ^5x_13x = ⁵₁₃ △ASB ~ △CSD h₁ = RS = RO+OS = r + 5x = r +⁵₁₃r = ¹⁸₁₃r h₂ = PS = OP−OS = r − 5x = r−⁵₁₃r = ⁸₁₃r skala podobieństwa:

	1813r
s =		= 1813*138=188 = 94
	813r

^a_b = ⁹₄ b = ⁴₉a △DMO ~ △OMA ^DM_OM=^OM_AM DM*AM = OM*OM ^b₂*^a₂ = r² a*b = 4r² a*⁴₉a=4r^{2 a2}₉ = r² a² = 9r² a = 3r −−−−−−−−−−−−−−−−− b = ⁴₉*3r b = ⁴₃r −−−−−−−−−−−−−−−−−− c = ^a₂+^b₂ = ³₂r + ⁴₆r = ³₂r + ²₃r = ⁹₆r + ⁴₆r = ¹³₆r c = ¹³₆r −−−−−−−−−−−−−−−−−−−−− L = a+b+2c = 3r + ⁴₃r + 2*¹³₆r = 3r + ⁴₃r + ¹³₃r L = ^9r+4r+13r₃ = ^26r₃ ^L_2πr = ^26r_6πr = ²⁶_6π = ¹³_3π No teraz już chyba bez błędu

@Basia: Już miałam odpuścić, ale doznałam olśnienia. Kilka razy się przymierzałam i nic mi nie wychodziło. A tu klik i jest. Dobranoc. Kolorowych snów