... nick: Jak rozwiązać taka nierówność

1
	> 1
lx−1l

rozpatrywać dwa przypadki x−1<0 i x−1≥0?

Artur_z_miasta_Neptuna: krok 1: założenia krok 2: mnożysz obustronnie przez |x−1| (w końcu jest to na pewno większe od 0) krok 3: rysujesz y=|x−1| krok 4: rysujesz y=1 krok 5: zaznaczasz części wykresu z krok 3, która jest PONIŻEJ wykresu prostej z kroku 4

nick: dzięki, a jest sposób "niegraficzny"?

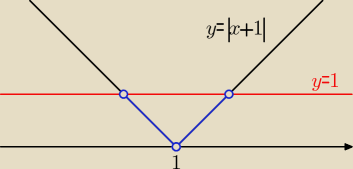
Artur_z_miasta_Neptuna: na niebiesko zaznaczony szukany część wykresu. czyli x∊(0;1)∪(1,2)

Artur_z_miasta_Neptuna: oczywiście że jest 'niegraficzny' dwa pierwsze kroki tak samo krok 3: przypadki |x−1| > 0 oraz |x−1| < 0

Artur_z_miasta_Neptuna: oczywiście tam bez wartości bezwzględnej te warunki

nick: dziękuję jeszcze raz

mycha: albo bez rysowania krok 1 i krok 2 taki sam. krok 3: rozwiązujemy otrzymaną nierówność: |x − 1| < 1 −1 < x − 1 < 1 i x ≠ 1 0 < x < 2 i x ≠ 1 x∊(0, 1)∪(1, 0)