Powierzchnia dachu Jacek: Jak obliczyć powierzchnię dachu w którym podstawa 2x3 m, a kąt nachylenia połaci wynosi 30°? Dach kopertowy (połacie to dwa trójkąty i dwa trapezy).

Artur z miasta Neptuna: A jaka dlugosc maja podstawy czesci trojkatnych? Albo jak wysoko wzosi soendasz wzgledem jego poczatku. albo jaka jest wysokosc ow trapezow i trojkatow (jezeli jest dachowka to mozna policzyc ile dachowek jest w pionie i pomnozyc razy ich dlugosc

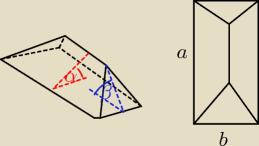
Artur_z_miasta_Neptuna: α = 30^o a=3m (tylko ) a jak 'położone' są trójkąty też pod kątem 30^o czy pod innym

Jacek: Zarówno trapezy jak i trójkąty są pod tym samym kątem. Jedyne dane to właśnie kąty nachylenia połaci (takie same; 30°) oraz wymiary podstawy (2m x 3m).

Ajtek: To zadanie ma dwa rozwiązania wg mnie.

Ajtek: Jednak ma jedno rozwiązanie, dłuższa krawędż jest podstawą trapezu.

Artur_z_miasta_Neptuna: Pole dachu = 2*P_trapezu + 2*P_Δ = (a+c)*H + b*H = (a+b+c)*H gdzie: a,c − podstawy trapezu (c szukana) b − podstawa trójkąta H − wysokość trapezu i trójkąta (jednakowe ze względu na taki sam kąt nachylenia) skoro oba są pod kątem 30 to:

	h
tg30o =		;
	d

gdzie: h −−− wysokość na jaką się wznosi dach (nie chodzi o wysokość trapezu tylko o realną różnicę pomiędzy wysokością budynku ) d −−− połowa długości boku trójkąta (połowa odległości pomiędzy podstawami dwóch przeciwległych trapezów) lub innymi słowy − rzut pionowy wysokości trapezu na podstawę dachu

	h		√3
tg30o =		= h ⇔ h =
	1		3

	h
c = 3 − 2*		= 3 − 2 = 1 /// mam nadzieję że wiesz skąd to ... jak nie to popatrz
	tg30o

na 'widok z góry' dachu ... c to jest górna podstawa trapezu ///

	h		h		√3		2		2√3
sin30o =		⇔ H =		=		*		=
	H		sin 30o		3		1		3

	2√3
Pdachu = (3+2+1)*		= 4√3 m
	3

+-: Tak na oko mało,4√3≈6,93 płaski 6m².

Artur_z_miasta_Neptuna: podstawa (płaska) ma 6m² (3*2)

	2
kąt nachylenia 30o oznacza że wysokość boku trapezu z '1' 'wydłuża' się do		≈ 1.155
	√3

więc masz 3*2*1,155 = 6,93 kąt nachylenia jest niewielki (30^o to praktycznie płaski dach) a więc i różnica nieznaczna (bo zaledwie 15.5%) pomiędzy powierzchnią dachu a jej podstawą.

+-: Zgadza się. Jak to to mówia: chłop na oko....

Jacek: Wielkie dzięki

Artur_z_miasta_Neptuna: można by się jeszcze pobawić i udowodnić, że: powierzchnia dachowa = powierzchni dachowej w kształcie dwóch prostokątów (bez bocznych trójkątów) = powierzchni dachowej spadowy (jeden prostokąt) ustawionymi po tym samym (30^o) kątem.

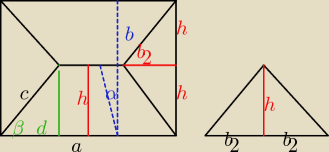
+-: Do Artur_zmiasta_Neptuna: Część trójkątna po przecięciu wzdłuż wysokości i ponownym złożeniu na wspólnym b/2 daje trójkąt wypełniający "rozpłaszczone trapezy" do prostokąta h=b/2cosα c²=b²/4 +h² d²=c²−h²=b²/4 +h²−h²=b²/4 d=b/2 czyli kąt β=45 co należało wcześniej przewidzieć P=2h*a=a*b/ cosα

Artur_z_miasta_Neptuna: spójrz na 12:53

Artur_z_miasta_Neptuna: chwila ... co to jest

Artur_z_miasta_Neptuna: skąd wiesz ile wynosi α kąt podstawy trójkąta ≠ kąta nachylenia trójkąta do podstawy dachu.

Artur_z_miasta_Neptuna: boże ... dopiero teraz załapałem rysunek okey ... wracamy do mojego postu z 12:53

+-: To jest w warunkach zadania, zresztą na Twoim rysunku też α. Mój rysunek pokazuje elementy dachu ułożone na powierzchni płaskiej natymiast kątα oraz b zaznaczone "przestrzennie"

nat..: Hala o wymiarach 19x20x5. Jaka bedzie powierzchnia dachu?