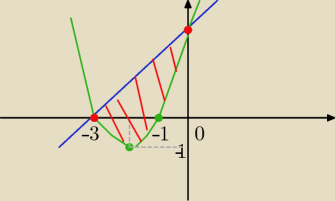
całka podwójna ograniczona funkcjami olek: ∫∫x dxdy , ograniczona y=x²+4x+3 i y=x+3, mam problem z wyliczeniem obszaru ograniczonego...mógłby mi ktos wytłumaczyć jak to się robi?

Artur z miasta Neptuna: http://www.wolframalpha.com/input/?i=plot%5By%3Dx2%2B4x%2B3%3B+y%3Dx%2B3%5D jak widać: x∊<−3 ; 0> y∊<x2+4x+3 ; x+3>

Artur z miasta Neptuna: oczywiście zapis jest zły ... bo trzeba to zapisać nierównościami ... ale ogólną 'wizję' powinieneś zauważyć

Eta:

olek: A w tym przypadku ? ∫∫(x³+3y²)dxdy ograniczone A(−1,0) B(0,1) C(1,0) x∊<0,1> y∊<x−1, −x+1>

	2		3
Wynik powinien wyjść		, a mi wychodzi podstawiając to
	3		5

gdzie robie bład?

Artur z miasta Neptuna: źle zrobiłeś granice całkowania albo: 0≤x≤1 ⋀ 0≤y≤x+1 + 0≤x≤1 ⋀ 0≤y≤−x+1 lub: y−1≤x≤−y+1 ⋀ 0≤y≤1 w te sposoby 'obrazujesz' tenże obszar

olek: sumując te całki wychodzi 4,5...

Artur z miasta Neptuna:

	x4
∫∫(x3 +3y2) dxdy = ∫ [		+ 3y2x](y−1)−(y−1) dy = ∫ −6y2(y−1) dy =
	4

∫(−6y³+6y²) dy =

	3y4		3		1
= [−		+ 2y3]01 = −		+ 2 =
	2		2		2

Artur z miasta Neptuna: przecież tam jest −1≤x≤1 powinno być: −1≤x≤0 ⋀ 0≤y≤x+1 + 0≤x≤1 ⋀ 0≤y≤−x+1

olek:

	2
Dzięki, widocznie w odpowiedziach zrobili bład. Bo za cholere nie chce wyjśc
	3

Artur z miasta Neptuna: nie wiem ... wpisz w wolframa

olek:

	1
na wolframie też wychodzi
	2