liniowa paweł: jak narysować wykres funkcji y=³₂x−2? i czy inne przykłady robi się analogicznie do tego?

Beti: wykresem każdej funkcji liniowej jest prosta, którą żeby narysować wystarczy wyznaczyć współrzędne dwóch punktów przez które ta prosta przejdzie, np:

	3
y =		x−2 −−> ta prosta przejdzie przez punkty: (0,−2) i (2,1)
	2

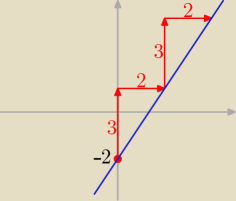
mycha: a tak

paweł: a jak wyznaczyć te współrzędne dwóch punktów?

Piotr: podstaw za x=0 i wylicz y podstaw za y=0 i wylicz x masz dwa punkty i do tego punkty przeciecia z osiami

mycha: y = ax + b

	3
zacznij od b (jest na osi y), potem 3 w górę i 2 w prawo, bo a =		,znowu 3 w górę
	2

i 2 w prawo i tak kilka razy, na koniec połącz wyznaczone punkty

Beti: wybierasz sobie dowolną liczbę(będzie to współrzędna x) i podstawiasz ją za x do wzoru funkcji −−> w ten sposób obliczysz y, czyli drugą współrzędną punktu. np.: x = 0

	3
i teraz: y =		*0 − 2 = −2
	2

więc: (0,−2) − jeden z puntów, przez który przejdzie prosta

Beti: dostałeś kilka różnych metod, któraś na pewno Ci podpasuje

Piotr: ja proponuję tak, bo czesto sie zdarza w poleceniu narysuj funkcje, a pozniej podaj wspolrzedne punktow przeciecia z osiami. no to wtedy ma zrobione dwa w jednym

paweł: bardzo dziękuje, na pewno postaram się zrozumieć. I tak wiem już więcej, niż wiedziałem

pigor: ... niech y=ax+b i a≠0 , czyli u ciebie y=³₂x−2 ⇒ gdy x=0 ⇒ y=b , a więc (0,b) − jeden punkt prostej i tak u ciebie jest to (0,−2), zaś gdy y=0 ⇒ ax+b=0 ⇔ x=−^b_a , czyli (−^b_a,0) − drugi punkt prostej i u ciebie jest to : 2 ³₂= 2*²₃ = ⁴₃ , czyli punkt (²₃,0) − nieciekawa odcięta (1−sza współrzędna) punktu , dlatego lepiej wziąć np. x=2 , wtedy y= 3−2=1 , czyli (2,1) − drugi punkt prostej . ...

Gustlik: Metoda "schodkowa", czyli jak zrobiła mycha, tu wyjaśniam, jak to zrobić: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=41.

Gustlik: Jeszcze raz link do metody "schodkowej" : https://matematykaszkolna.pl/forum/forum.py?komentarzdo=41